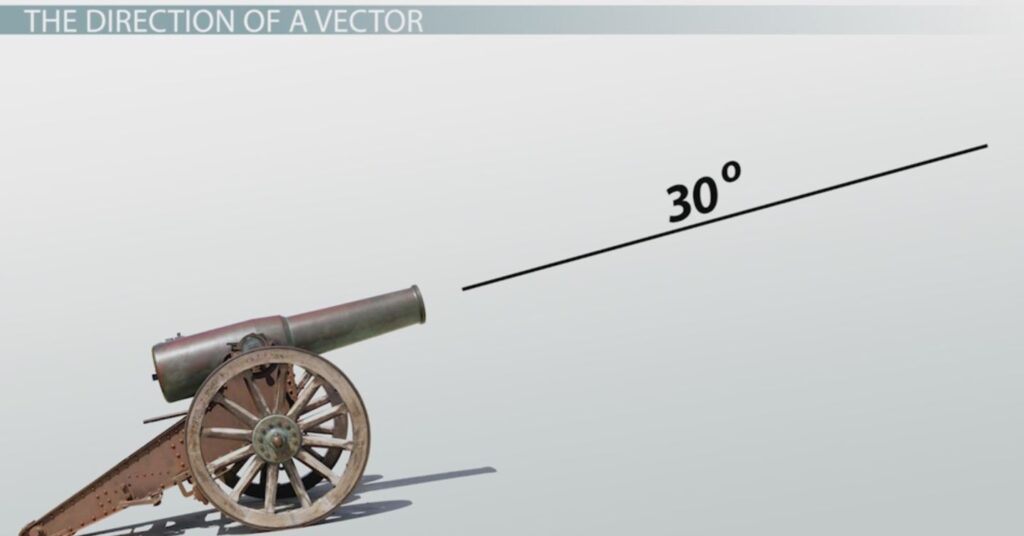
The above discussion explains the method for determining the magnitude of the resultant for three or more perpendicular vectors. The topic of direction has been ignored in the discussion. Now we will turn our attention to the method for determining the direction of the resultant vector. As a quick review, recall that earlier in this lesson a convention for expressing the direction of a vector was introduced. The convention is known as the counter-clockwise from east convention, often abbreviated as the CCW convention. Using this convention, the direction of a vector is often expressed as a counter-clockwise angle of rotation of the vector about its tail from due East.

To begin our discussion, let’s return to Example 1 above where we made an effort to add three vectors: 6.0 km, N + 6.0 km, E + 2.0 km, N. In the solution, the order of addition 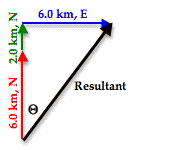of the three vectors was rearranged so that a right triangle was formed with the resultant being the hypotenuse of the triangle. The triangle is redrawn at the right. Observe that the angle in the lower left of the triangle has been labeled as theta (Θ). Theta (Θ) represents the angle that the vector makes with the north axis. Theta (Θ) can be calculated using one of the three trigonometric functions introduced earlier in this lesson – sine, cosine or tangent. The mnemonic SOH CAH TOA is a helpful way of remembering which function to use. In this problem, we wish to determine the angle measure of theta (Θ) and we know the length of the side opposite theta (Θ) – 6.0 km – and the length of the side adjacent the angle theta (Θ) – 8.0 km. The TOA of SOH CAH TOA indicates that the tangent of any angle is the ratio of the lengths of the side opposite to the side adjacent that angle. Thus, the tangent function will be used to calculate the angle measure of theta (Θ). The work is shown below.
 

Tangent(Θ) = Opposite/Adjacent
Tangent(Θ) = 6.0/8.0
Tangent(Θ) = 0.75
Θ = tan^-1 (0.75)
Θ = 36.869 …°
Θ =37°

The problem is not over once the value of theta (Θ) has been calculated. This angle measure must now be used to state the direction. One means of doing so is to simply state that the direction of the resultant is 37° east of north. Alternatively, the counter-clockwise convention could be used. Since the angle that the resultant makes with east is the complement of the angle that it makes with north, we could express the direction as 53° CCW.

We will now consider Example 2 as a second example of how to use SOH CAH TOA to determine the direction of a resultant. In Example 2, we were trying to determine the magnitude of 2.0 m. S + 16.0 m, W + 24.0 m, N + 36.0 m, W. The solution involved re-ordering the addition so that the resultant was the hypotenuse of a right triangle with known sides. The right triangle is shown below. The resultant is drawn in black. Once more, observe that the angle in the lower right of the triangle has been labeled as theta (Θ). Theta (Θ) represents the angle that the vector makes with the north axis.
 

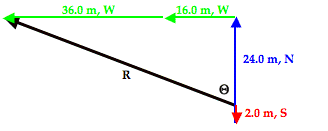
Theta (Θ) can be calculated using the tangent function. In this problem, we wish to determine the angle measure of theta (Θ) and we know the length of the side opposite theta (Θ) – 52.0 m – and the length of the side adjacent the angle theta (Θ) – 22.0 m. The TOA of SOH CAH TOA indicates that the tangent of any angle is the ratio of the lengths of the side opposite to the side adjacent that angle. Thus, the tangent function will be used to calculate the angle measure of theta (Θ). The work is shown below.

Tangent(Θ) = Opposite/Adjacent
Tangent(Θ) = 52.0/22.0
Tangent(Θ) = 2.3636 …
Θ = tan^-1 (2.3636 …)
Θ = 67.067 …°
Θ =67.1°

The problem is not over once the value of theta (Θ) has been calculated. This angle measure must now be used to state the direction. One means of doing so is to simply state that the direction of the resultant is 67.1° west of north. Alternatively, the counter-clockwise convention could be used. The north axis is rotated 90° counter-clockwise from east and this vector is an additional 67.1° counter-clockwise past north. Thus the CCW direction is 157.1° CCW.

In summary, the direction of a vector can be determined in the same way that it is always determined – by finding the angle of rotation counter-clockwise from due east. Since the resultant is the hypotenuse of a right triangle, this can be accomplished by first finding an angle that the resultant makes with one of the nearby axes of the triangle. Once done, a little thinking is required in order to relate the angle to a direction.