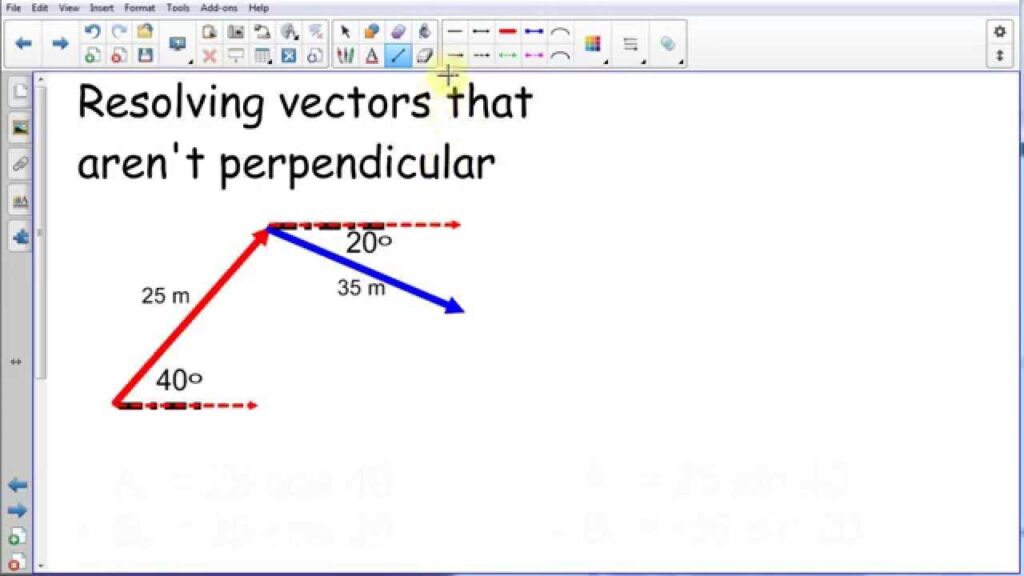
Now we will consider situations in which the two (or more) vectors that are being added are not at right angles to each other. The Pythagorean theorem is not applicable to such situations since it applies only to right triangles. Two non-perpendicular vectors will not form a right triangle. Yet it is possible to force two (or more) non-perpendicular vectors to be transformed into other vectors that do form a right triangle. The trick involves the concept of a vector component and the process of vector resolution.
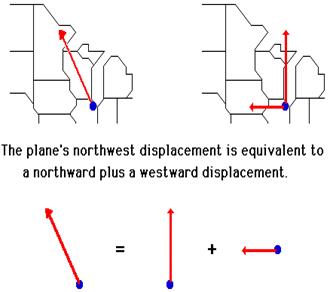
A vector component describes the effect of a vector in a given direction. Any angled vector has two components; one is directed horizontally and the other is directed vertically. For instance, a northwest vector has a northward component and a westward component. Together, the effect these two components are equal to the overall effect of the angled vector. As an example, consider a plane that flies northwest from Chicago O’Hare airport towards the Canada border. The northwest displacement vector of the plane has two components – a northward component and a westward component. When added together, these two components are equal to the overall northwest displacement. This is shown in the diagram below.
The northwest vector has north and west components that are represented as Ax and Ay. It can be said that
A = Ax + Ay
So whenever we think of a northwest vector, we can think instead of two vectors – a north and a west vector. The two components Ax + Ay can be substituted in for the single vector A in the problem.
Now suppose that your task involves adding two non-perpendicular vectors together. We will call the vectors A and B. Vector A is a nasty angled vector that is neither horizontal nor vertical. And vector B is a nice, polite vector directed horizontally. The situation is shown below.
Of course nasty vector A has two components – Ax and Ay. These two components together are equal to vector A. That is, A = Ax + Ay .
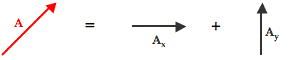
And since this is true, it makes since to say that A + B = Ax + Ay + B.
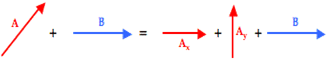
And so the problem of A + B has been transformed into a problem in which all vectors are at right angles to each other. Nasty has been replaced by nice and that should make any physics student happy. With all vectors being at right angles to one another, their addition leads to a resultant that is at the hypotenuse of a right triangle. The Pythagorean theorem can then be used to determine the magnitude of the resultant.
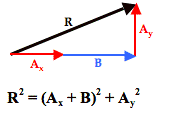
To see how this process works with an actual vector addition problem, consider Example 3 shown below.
Example 3:
Max plays middle linebacker for South’s football team. During one play in last Friday night’s game against New Greer Academy, he made the following movements after the ball was snapped on third down. First, he back-pedaled in the southern direction for 2.6 meters. He then shuffled to his left (west) for a distance of 2.2 meters. Finally, he made a half-turn and ran downfield a distance of 4.8 meters in a direction of 240° counter-clockwise from east (30° W of S) before finally knocking the wind out of New Greer’s wide receiver. Determine the magnitude and direction of Max’s overall displacement.
As is the usual case, the solution begins with a diagram of the vectors being added.
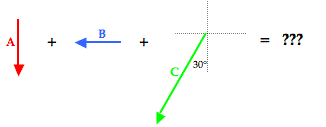
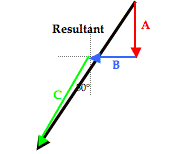To assist in the discussion, the three vectors have been labeled as vectors A, B, and C. The resultant is the vector sum of these three vectors; a head-to-tail vector addition diagram reveals that the resultant is directed southwest. Of the three vectors being added, vector C is clearly the nasty vector. Its direction is neither due south nor due west. The solution involves resolving this vector into its components.
The process of vector resolution was discussed earlier in this lesson. The process involves using the magnitude and the sine and cosine functions to determine the x- and y-components of the vector. Vector C makes a 30° angle with the southern direction. By sketching a right triangle with horizontal and vertical legs and C as the hypotenuse, it becomes possible to determine the components of vector C. This is shown in the diagram below. The side adjacent this 30° angle in the triangle is the vertical side; the vertical side represents the vertical (southward) component of C – Cy. So to determine Cy, the cosine function is used. The side opposite the 30° angle is the horizontal side; the horizontal side represents the horizontal (westward) component of C – Cx. The values of Cx and Cy can be determined by using SOH CAH TOA. The cosine function is used to determine the southward component since the southward component is adjacent to the 30° angle. The sine function is used to determine the westward component since the westward component is the side opposite to the 30° angle. The work is shown below.
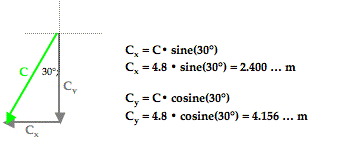
Now our vector addition problem has been transformed from the addition of two nice vectors and one nasty vector into the addition of four nice vectors.
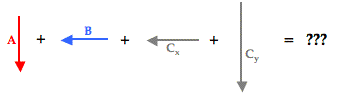
With all vectors oriented along are customary north-south and east-west axes, they can be added head-to-tail in any order to produce a right triangle whose the hypotenuse is the resultant. Such a diagram is shown below.
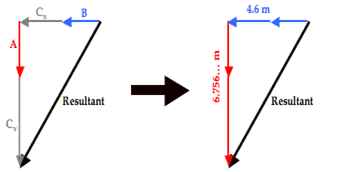
The triangle’s perpendicular sides have lengths of 4.6 meters and 6.756 meters. The length of the horizontal side (4.6 m) was determined by adding the values of B (2.2 m) and Cx (2.4 m). The length of the vertical side (6.756… m) was determined by adding the values of A (2.6 m) and Cy (4.156… m). The resultant’s magnitude (R) can now be determined using the Pythagorean theorem.
R2 = (6.756… m)2 + (4.6 m)2
R2 = 45.655… m2 + 21.16 m2
R2 = 66.815… m2
R = SQRT(66.815… m2 )
R = 8.174 … m
R = ~8.2 m
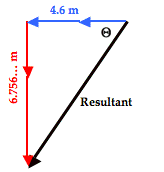The direction of the resultant can be determined by finding the angle that the resultant makes with either the north-south or the east-west vector. The diagram at the right shows the angle theta (Θ) marked inside the vector addition triangle. This angle theta is the angle that the resultant makes with west. Its value can be determined using the tangent function. The tangent function (as in TOA) relates the angle value to the ratio of the lengths of the opposite side to the adjacent side. That is,
Tangent (Θ) = (6.756… m)/(4.6 m) = 1.46889…
Using the inverse tangent function, the angle theta (Θ) can be determined. On most calculators, this involves using the 2nd-Tangent buttons.
Θ = tan-1 (1.46889…) = 55.7536… °
Θ = ~56°
This 56° angle is the angle between the resultant vector (drawn in black above) and the westward direction. This makes the direction 56° south of west. The direction of the resultant based on the counter-clockwise from east convention (CCW) can be determined by adding 180° to the 56°. So the CCW direction is 236°.
Example 4 provides one final example of how to combine vector resolution with vector addition in order to add three or more non-perpendicular vectors. Because this example includes three particularly nasty vectors, a table will be used to organize the information about he magnitude and direction of the components. The use of a table is a wise idea when problems get complicated.
Example 4:
Cameron Per (his friends call him Cam) and Baxter Nature are on a hike. Starting from home base, they make the following movements.
A: 2.65 km, 140° CCW
B: 4.77 km, 252° CCW
C: 3.18 km, 332° CCW
Determine the magnitude and direction of their overall displacement.
The visual representation of the situation is shown below.
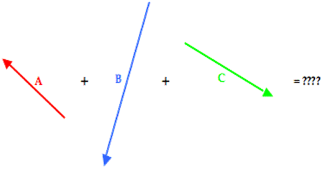
To determine the resultant, the three individual vectors are resolved into horizontal and vertical components. The angle information about each vector is used to form a right triangle in which the vector is the hypotenuse and the perpendicular sides are oriented along the east-west and north-south axes. This is shown in the diagram below.
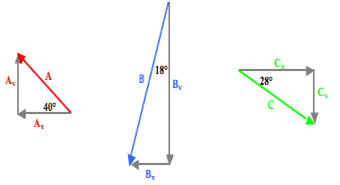
Trigonometric functions – sine, cosine and tangent – are then used to determine the magnitude of the horizontal and vertical component of each vector. The work is shown and organized in the table below.
| Vector | East-West Component | North-South Component |
A 2.65 km 140° CCW | (2.65 km)•cos(40°) = 2.030… km, West | (2.65 km)•sin(40°) = 1.703… km, North |
B 4.77 km 252° CCW | (4.77 km)•sin(18°) = 1.474… km, West | (4.77 km)•cos(18°) = 4.536… km, South |
C 3.18 km 332° CCW | (3.18 km)•cos(28°) = 2.808… km, East | (3.18 km)•sin(28°) = 1.493… km, South |
Sum of A + B + C | 0.696 km, West | 4.326 km, South |
The last row of the above table represents the sum of all the East-West components and the sum of all the North-South components. The resultant consists of these two components. The resultant is determined by adding together these two the components to form a right triangle that has a hypotenuse that is equal to the resultant. This typically involves adding all the horizontal components to determine the total length of the horizontal side of the right triangle … and adding all the vertical components to determine the total length of the vertical side of the right triangle. This is done in the table above by simple adding another row to the table for the vector sum of all the components. In adding the east-west components of all the individual vectors, one must consider that an eastward component and a westward component would add together as a positive and a negative. Some students prefer to think of this as subtraction as opposed to addition. In actuality, it really is addition – the addition of vectors with opposite direction. Similarly, a northward and a southward component would also add together as a positive and a negative. Once the bottom row is accurately determined, the magnitude of the resultant can be determined using Pythagorean theorem.
R2 = (0.696 km)2 + (4.326 km)2
R2 = 0.484 km2 + 18.714 km2
R2 = 19.199 km2
R = SQRT(19.199 km2)
R = ~4.38 km
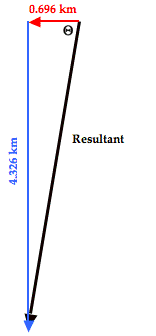The direction of the resulting displacement can be determined by constructing the final triangle from the components of the resultant. The components of the resultant are simply the sum the east-west and north-south components. Once done, SOH CAH TOA is used to determine the angle that the resultant makes with a nearby axis. The diagram is shown at the right. The angle labeled as theta (Θ) is the angle between the resultant vector and the west axis. This angle can be calculated as follows:
Tangent(Θ) = opposite/adjacent
Tangent(Θ) = (4.326 km)/(0.696 km)
Tangent(Θ) = 6.216
Θ = tan-1(6.216)
Θ = 80.9°
This angle measure represents the angle of rotation of the vector south of due west. It would be worded as 80.9° south of west. Since west is 180° counterclockwise from east, the direction could also be expressed in the counterclockwise (CCW) from east convention as 260.9°.
So the result of our analysis is that the overall displacement is 4.38 km with a direction of 260.9° (CCW).
