As our first example, consider the following vector addition problem:
Example 1:
A student drives his car 6.0 km, North before making a right hand turn and driving 6.0 km to the East. Finally, the student makes a left hand turn and travels another 2.0 km to the north. What is the magnitude of the overall displacement of the student?
Like any problem in physics, a successful solution begins with the development of a mental picture of the situation. The construction of a diagram like that below often proves useful in the visualization process.

When these three vectors are added together in head-to-tail fashion, the resultant is a vector that extends from the tail of the first vector (6.0 km, North, shown in red) to the arrowhead of the third vector (2.0 km, North, shown in green). The head-to-tail vector addition diagram is shown below.
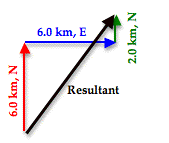
As can be seen in the diagram, the resultant vector (drawn in black) is not the hypotenuse of any right triangle – at least not of any immediately obvious right triangle. But would it be possible to force this resultant vector to be the hypotenuse of a right triangle? The answer is Yes! To do so, the order in which the three vectors are added must be changed. The vectors above were drawn in the order in which they were driven. The student drove north, then east, and then north again. But if the three vectors are added in the order 6.0 km, N + 2.0 km, N + 6.0 km, E, then the diagram will look like this:
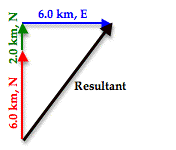
After rearranging the order in which the three vectors are added, the resultant vector is now the hypotenuse of a right triangle. The lengths of the perpendicular sides of the right triangle are 8.0 m, North (6.0 km + 2.0 km) and 6.0 km, East. The magnitude of the resultant vector (R) can be determined using the Pythagorean theorem.
R2 = (8.0 km)2 + (6.0 km)2
R2 = 64.0 km2+ 36.0 km2
R2 = 100.0 km2
R = SQRT (100.0 km2)
R = 10.0 km
(SQRT indicates square root)
In the first vector addition diagram above, the three vectors were added in the order in which they are driven. In the second vector addition diagram (immediately above), the order in which the vectors were added was switched around. The size of the resultant was not affected by this change in order. This illustrates an important point about adding vectors: the resultant is independent by the order in which they are added. Adding vectors A + B + C gives the same resultant as adding vectors B + A + C or even C + B + A. As long as all three vectors are included with their specified magnitude and direction, the resultant will be the same. This property of vectors is the key to the strategy used in the determination of the answer to the above example problem. To further illustrate the strategy, let’s consider the vector addition situation described in Example 2 below.
Example 2:
Mac and Tosh are doing the Vector Walk Lab. Starting at the door of their physics classroom, they walk 2.0 meters, south. They make a right hand turn and walk 16.0 meters, west. They turn right again and walk 24.0 meters, north. They then turn left and walk 36.0 meters, west. What is the magnitude of their overall displacement?
A graphical representation of the given problem will help visualize what is happening. The diagram below depicts such a representation.
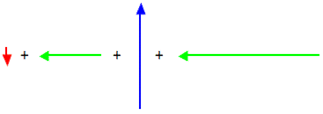
When these four vectors are added together in head-to-tail fashion, the resultant is a vector that extends from the tail of the first vector (2.0 m, South, shown in red) to the arrowhead of the fourth vector (36.0 m, West, shown in green). The head-to-tail vector addition diagram is shown below.
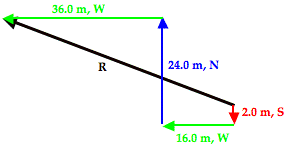
The resultant vector (drawn in black and labeled R) in the vector addition diagram above is not the hypotenuse of any immediately obvious right trangle. But by changing the order of addition of these four vectors, one can force this resultant vector to be the hypotenuse of a right triangle. For instance, by adding the vectors in the order of 2.0 m, S + 24.0 m, N + 16.0 m, W + 36.0 m. W, the resultant becomes the hypotenuse of a right triangle. This is shown in the vector addition diagram below.
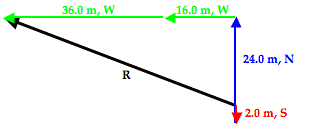
With the vectors rearranged, the resultant is now the hypotenuse of a right triangle that has two perpendicular sides with lengths of 22.0 m, North and 52.0 m, West. The 22.0 m, North side is the result of 2.0 m, South and 24.0 m, North added together. The 52.0 m, West side is the result of 16.0 m, West and 36.0 m, West added together. The magnitude of the resultant vector (R) can be determined using the Pythagorean theorem.
R2 = (22.0 m)2 + (52.0 m)2
R2 = 484.0 m2 + 2704.0 m2
R2 = 3188.0 m2
R = SQRT (3188.0 m22)
R = 56.5 m
(SQRT indicates square root)
As can be seen in these two examples, the resultant of the addition of three or more right angle vectors can be easily determined using the Pythagorean theorem. Doing so involves the adding of the vectors in a different order.