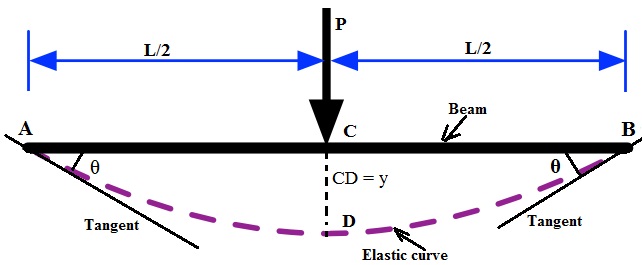
a)      When a beam with a straight longitudinal axis is loaded by lateral forces, the axis is deformed into a curve, called the deflection curve of the beam.

b)      Most procedures for finding beam deflections are based on the differential equations of the deflection curve and their associated relationships.

c)      Consider a cantilever beam with a concentrated load acting upward at the free end.

i)        Due to this load, the axis of the beam deforms into a curve

ii)      The reference axes have their origin at the fixed end of the beam

iii)    x axis directed to the right and the y axis directed upward.

iv)    z axis is directed outward from the figure (toward the viewer).

v)      xy plane is a plane of symmetry of the beam

vi)    all loads act in this plane (the plane of bending)

d)      The deflection v is the displacement in the y direction of any point on the axis of the beam