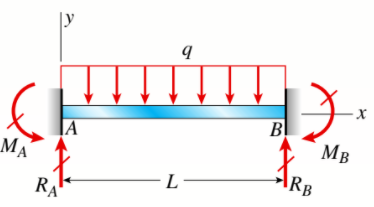
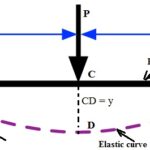
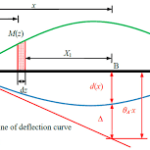
a.)    To obtain the equation of the deflection curve, we must express the deflection vas a function of the coordinate x.

b.) When the beam is bent, there is not only a deflection at each point along the axis but also a rotation.

The angle of rotation θ (angle of inclination or angle of slope) of the axis of the beam is the angle between the x axis and the tangent to the deflection curve. ρ is radius of curvature and  iscurvature. Sign convention of curvature is positive when the angle of rotation increases as we move along the beam in the positive x direction. Since 

From above diagram on the right side we can see that. Also θ is very small so 

From above two equations we get

This equation is valid for a beam of any material, provided the rotations are small quantities.

If the material of a beam is linearly elastic and follows Hooke’s law, the curvature then

Therefore combining equations we get Differential equation of the deflection curve

We know that  and  so we can write above equation in other forms

Bending –moment equation	Shear-force equation	Load equation
or	V     or	or

Deflections by integration of the bending-moment equation

a.) Equation is of second order, two integrations are required. The first integration produces the slope  and the second produces the deflection v.

b.)  Procedure

                                                              i.      In some cases a single bending-moment expression holds for the entire length of the beam

                                                            ii.      In other cases the bending moment changes abruptly at one or more points along the axis of the beam. Then we must write separate bending-moment expressions for each region of the beam between points where changes occur

                                                          iii.      Regardless of the number of bending-moment expressions, the general procedure for solving the differential equations

1.      For each region of the beam, we substitute the expression for M found out from equation of equilibrium into the differential equation and integrate to obtain the slope. Each such integration produces one constant of integration.

2.    Next integrate each slope equation to obtain the corresponding deflection v. Each integration produces a new constant

3.    Thus, there are two constants of integration for each region of the beam. So if there are two region of beam (two equation of M for same beam) there will be four constants.

4.      These constants are evaluated from known conditions pertaining to the slopes and deflections. The conditions fall into three categories: (1) boundary conditions, (2) continuity conditions, and (3) symmetry conditions

Boundary conditions	Continuity conditions	Symmetry conditions
Deflections and slopes at thesupports of a beam	Points where the regions of integration meet	If a simple beam supports a uniform load throughout its length, we know in advance that the slope of the deflection curve at the midpoint must be zero.
Deflection is zero at the supports

The preceding method for finding deflections is sometimes called the method of successive integrations.