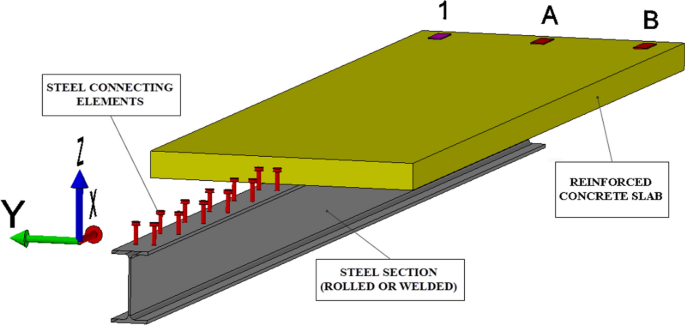
a)      Beams that are fabricated of more than one material are called composite beams.

b)      

ii)      Assumptions

(1)   xy plane is a plane of symmetry

(2)   xz plane is the neutral plane of the beam

iii)    But the neutral axis does not pass through the centroid of the cross-sectional area when the beam is made of two different materials

c)    Location of neutral axis

 is same hence removed)

i)        If the cross section of a beam is doubly symmetric, as in the case of a wood beam with steel cover plates on the top and bottom, the neutral axis is located at the mid-height of the cross section and above equation is not needed

d)   Moment-Curvature relationship

Again the integration is performed over two areas

e)    Flexure formula for a composite beam

i)        Now combining Moment-Curvature equation and Normal Stresses In Beams we will get

f)    Transformed Section method

i)        The transformed-section method is an alternative procedure for analyzing the bending stresses in a composite beam.

ii)      The method consists of

(1)   Transforming the cross section of a composite beam into an equivalent cross section of an imaginary beam that is composed of only one material. This new cross section is called the transformed section.

(2)   Then the imaginary beam with the transformed section is analyzed in the customary manner for a beam of one material.

(3)   The stresses in the transformed beam are converted to those in the original beam.

iii) 

The neutral axis is unchanged if each element of area dA in material 2 is multiplied by the factor n, provided that the y coordinate for each such element of area is not changed.

Therefore, we can create a new cross section consisting of two parts: (1) area 1 with its dimensions unchanged, and (2) area 2 with its width (that is, its dimension parallel to the neutral axis) multiplied by n.

iv)  Analysis of transformed section

(1)   Location of neutral axis is found exactly like beam made up of one material

(2)   Formula for Moment remain same

(3)   Formula for stress

Let  moment of inertia of the transformed section with respect to the neutral axis

The stresses in material 2 in the original beam are not the same as the stresses in the corresponding part of the transformed beam. Instead, the stresses in the transformed beam must be multiplied by the modular ratio n to obtain the stresses in material 2 of the original beam.