a)      When a beam is in pure bending, the only stress resultants are the bending moments and the only stresses are the normal stresses acting on the cross sections. However, most beams are subjected to loads that produce both bending moments and shear forces (nonuniform bending). In these cases, both normal and shear stresses are developed in the beam.

From last diagram we can write

Now

If the shear stresses  are uniformly distributed across the width b of the beam, the force F₃ is also equal to the following

Now we know that  and  first moment of area

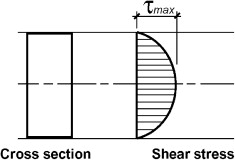
This equation, known as the shear formula, can be used to determine the shear stress  at any point in the cross section of a rectangular beam. Note that for a specific cross section, the shear force V, moment of inertia I and width b are constants. However, the first moment Q (and hence the shear stress) varies with the distance y₁ from the neutral axis.

b)      Calculation of the First Moment Q

We usually use the area above the level y₁ when the point where we are finding the shear stress is in the upper part of the beam, and we use the area below the level y₁ when the point is in the lower part of the beam.