Estimates of the radii of most metal atoms can be found. Where do these data come from? How do we know, for example, that the radius of a nickel atom is 0.1246 nm?

Nickel crystallizes in a face-centered cubic unit cell with a cell-edge length of 0.3524 nm to calculate the radius of a nickel atom.

One of the faces of a face-centered cubic unit cell is shown in the figure below.

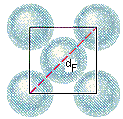
According to this figure, the diagonal across the face of this unit cell is equal to four times the radius of a nickel atom.

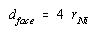
The Pythagorean theorem states that the diagonal across a right triangle is equal to the sum of the squares of the other sides. The diagonal across the face of the unit cell is therefore related to the unit-cell edge length by the following equation.

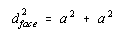
Taking the square root of both sides gives the following result.

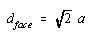
We now substitute into this equation the relationship between the diagonal across the face of this unit cell and the radius of a nickel atom:

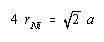
Solving for the radius of a nickel atom gives a value of 0.1246 nm:

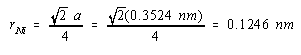
A similar approach can be taken to estimating the size of an ion. Let’s start by using the fact that the cell-edge length in cesium chloride is 0.4123 nm to calculate the distance between the centers of the Cs⁺ and Cl^– ions in CsCl.

CsCl crystallizes in a simple cubic unit cell of Cl^– ions with a Cs⁺ ion in the center of the body of the cell, as shown in the figure below.

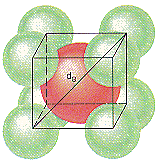
Before we can calculate the distance between the centers of the Cs⁺ and Cl^– ions in this crystal, however, we have to recognize the validity of one of the simplest assumptions about ionic solids: The positive and negative ions that form these crystals touch.

We can therefore assume that the diagonal across the body of the CsCl unit cell is equivalent to the sum of the radii of two Cl^– ions and two Cs⁺ ions.

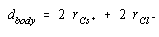
The three-dimensional equivalent of the Pythagorean theorem suggests that the square of the diagonal across the body of a cube is the sum of the squares of the three sides.

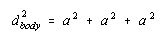
Taking the square root of both sides of this equation gives the following result.

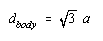
If the cell-edge length in CsCl is 0.4123 nm, the diagonal across the body in this unit cell is 0.7141 nm.

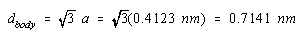
The sum of the ionic radii of Cs⁺ and Cl^– ions is half this distance, or 0.3571 nm.

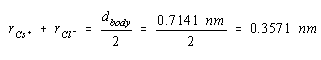
If we had an estimate of the size of either the Cs⁺ or Cl^– ion, we could use the results to calculate the radius of the other ion. The ionic radius of the Cl^– ion is 0.181 nm. Substituting this value into the last equation gives a value of 0.176 nm for the radius of the Cs⁺ ion.

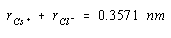
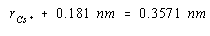
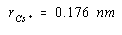
The results of this calculation are in reasonable agreement with the value of 0.169 nm known for the radius of the Cs⁺ ion. The discrepancy between these values reflects the fact that ionic radii vary from one crystal to another. The tabulated values are averages of the results of a number of calculations of this type.