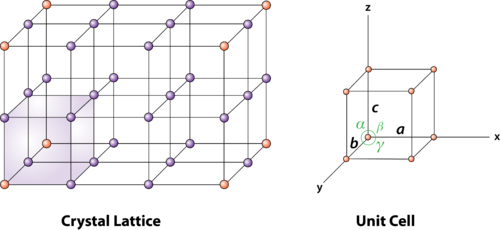
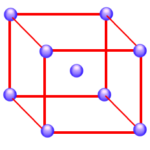
Atoms on the corners, edges, and faces of a unit cell are shared by more than one unit cell, as shown in the figure below. An atom on a face is shared by two unit cells, so only half of the atom belongs to each of these cells. An atom on an edge is shared by four unit cells, and an atom on a corner is shared by eight unit cells. Thus, only one-quarter of an atom on an edge and one-eighth of an atom on a corner can be assigned to each of the unit cells that share these atoms.

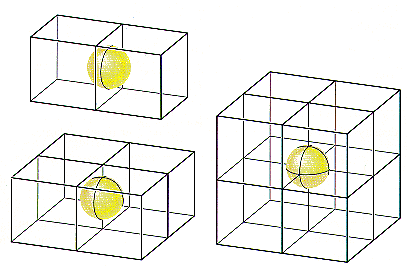
If nickel crystallized in a simple cubic unit cell, there would be a nickel atom on each of the eight corners of the cell. Because only one-eighth of these atoms can be assigned to a given unit cell, each unit cell in a simple cubic structure would have one net nickel atom.

Simple cubic structure:

8 corners x 1/8 = 1 atom

If nickel formed a body-centered cubic structure, there would be two atoms per unit cell, because the nickel atom in the center of the body wouldn’t be shared with any other unit cells.

Body-centered cubic structure:

(8 corners x 1/8) + 1 body = 2 atoms

If nickel crystallized in a face-centered cubic structure, the six atoms on the faces of the unit cell would contribute three net nickel atoms, for a total of four atoms per unit cell.

Face-centered cubic structure:

(8 corners x 1/8) + (6 faces x 1/2) = 4 atoms

Because they have different numbers of atoms in a unit cell, each of these structures would have a different density. Let’s therefore calculate the density for nickel based on each of these structures and the unit cell edge length for nickel given in the previous section: 0.3524 nm. In order to do this, we need to know the volume of the unit cell in cubic centimeters and the mass of a single nickel atom.

The volume (V) of the unit cell is equal to the cell-edge length (a) cubed.

V = a³ = (0.3524 nm)³ = 0.04376 nm³

Since there are 10⁹ nm in a meter and 100 cm in a meter, there must be 10⁷ nm in a cm.

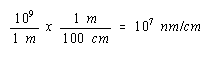
We can therefore convert the volume of the unit cell to cm³ as follows.

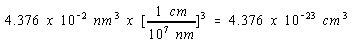
The mass of a nickel atom can be calculated from the atomic weight of this metal and Avogadro’s number.

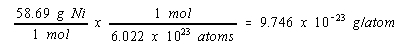
The density of nickel, if it crystallized in a simple cubic structure, would therefore be 2.23 g/cm³, to three significant figures.

Simple cubic structure:

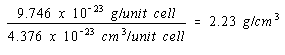
Because there would be twice as many atoms per unit cell if nickel crystallized in a body-centered cubic structure, the density of nickel in this structure would be twice as large.

Body-centered cubic structure:

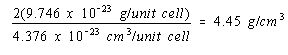
There would be four atoms per unit cell in a face-centered cubic structure and the density of nickel in this structure would be four times as large.

Face-centered cubic structure:

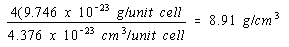
The experimental value for the density of nickel is 8.90 g/cm³. The obvious conclusion is that nickel crystallizes in a face-centered cubic unit cell and therefore has a cubic closest-packed structure.