NaCl should crystallize in a cubic closest-packed array of Cl– ions with Na+ ions in the octahedral holes between planes of Cl– ions. We can translate this information into a unit-cell model for NaCl by remembering that the face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure.
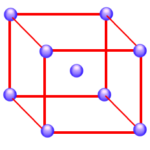
There are four unique positions in a face-centered cubic unit cell. These positions are defined by the coordinates: 0,0,0; 0,1/2,1/2; 1/2,0,1/2; and 1/2,1/2,0. The presence of an particle at one corner of the unit cell (0,0,0) requires the presence of an equivalent particle on each of the eight corners of the unit cell. Because the unit-cell edge connects equivalent points, the presence of a particle in the center of the bottom face (0,1/2,1/2) implies the presence of an equivalent particle in the center of the top face (1,1/2,1/2). Similarly, the presence of particles in the center of the 1/2,0,1/2 and 1/2,1/2,0 faces of the unit cell implies equivalent particles in the centers of the 1/2,1,1/2 and 1/2,1/2,1 faces.
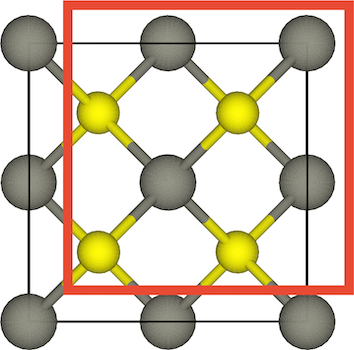
The figure below shows that there is an octahedral hole in the center of a face-centered cubic unit cell, at the coordinates 1/2,1/2,1/2. Any particle at this point touches the particles in the centers of the six faces of the unit cell.
The other octahedral holes in a face-centered cubic unit cell are on the edges of the cell, as shown in the figure below.
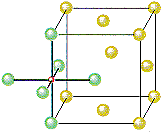
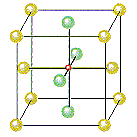
If Cl– ions occupy the lattice points of a face-centered cubic unit cell and all of the octahedral holes are filled with Na+ ions, we get the unit cell shown in the figure below.
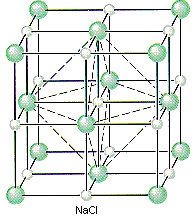
We can therefore describe the structure of NaCl in terms of the following information.
- NaCl crystallizes in a cubic unit cell.
- The cell-edge length is 0.5641 nm.
- There are Cl– ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Na+ ions at the positions 1/2,1/2,1/2; 1/2,0,0; 0,1/2,0; and 0,0,1/2.
Placing a Cl– ion at these four positions implies the presence of a Cl– ion on each of the 14 lattice points that define a face-centered cubic unit. Placing a Na+ ion in the center of the unit cell (1/2,1/2,1/2) and on the three unique edges of the unit cell (1/2,0,0; 0,1/2,0; and 0,0,1/2) requires an equivalent Na+ ion in every octahedral hole in the unit cell.
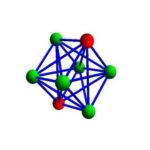
ZnS crystallizes as cubic closest-packed array of S2- ions with Zn2+ ions in tetrahedral holes. The S2- ions in this crystal occupy the same positions as the Cl– ions in NaCl. The only difference between these crystals is the location of the positive ions. The figure below shows that the tetrahedral holes in a face-centered cubic unit cell are in the corners of the unit cell, at coordinates such as 1/4,1/4,1/4. An atom with these coordinates would touch the atom at this corner as well as the atoms in the centers of the three faces that form this corner. Although it is difficult to see without a three-dimensional model, the four atoms that surround this hole are arranged toward the corners of a tetrahedron.
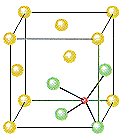
Because the corners of a cubic unit cell are identical, there must be a tetrahedral hole in each of the eight corners of the face-centered cubic unit cell. If S2- ions occupy the lattice points of a face-centered cubic unit cell and Zn2+ ions are packed into every other tetrahedral hole, we get the unit cell of ZnS shown in the figure below.
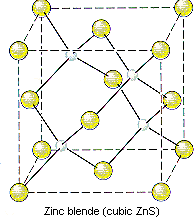
The structure of ZnS can therefore be described as follows.
- ZnS crystallizes in a cubic unit cell.
- The cell-edge length is 0.5411 nm.
- There are S2- ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Zn2+ ions at the positions 1/4,1/4,1/4; 1/4,3/4,3/4; 3/4,1/4,3/4; and 3/4,3/4,1/4.
Note that only half of the tetrahedral holes are occupied in this crystal because there are two tetrahedral holes for every S2- ion in a closest-packed array of these ions.