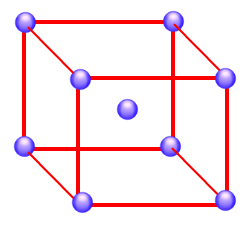
Nickel is one of the metals that crystallize in a cubic closest-packed structure. When you consider that a nickel atom has a mass of only 9.75 x 10^-23 g and an ionic radius of only 1.24 x 10^-10 m, it is a remarkable achievement to be able to describe the structure of this metal. The obvious question is: How do we know that nickel packs in a cubic closest-packed structure?

The only way to determine the structure of matter on an atomic scale is to use a probe that is even smaller. One of the most useful probes for studying matter on this scale is electromagnetic radiation.

In 1912, Max van Laue found that x-rays that struck the surface of a crystal were diffracted into patterns that resembled the patterns produced when light passes through a very narrow slit. Shortly thereafter, William Lawrence Bragg, who was just completing his undergraduate degree in physics at Cambridge, explained van Laue’s resultswith an equation known as the Bragg equation, which allows us to calculate the distance between planes of atoms in a crystal from the pattern of diffraction of x-rays of known wavelength.

n = 2d sin T

The pattern by which x-rays are diffracted by nickel metal suggests that this metal packs in a cubic unit cell with a distance between planes of atoms of 0.3524 nm. Thus, the cell-edge length in this crystal must be 0.3524 nm. Knowing that nickel crystallizes in a cubic unit cell is not enough. We still have to decide whether it is a simple cubic, body-centered cubic, or face-centered cubic unit cell. This can be done by measuring the density of the metal.