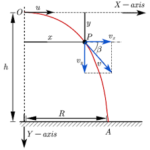
A non-horizontally launched projectile with an initial vertical velocity of 39.2 m/s will reach its peak in 4 seconds. The process of rising to the peak is a vertical motion and is again dependent upon vertical motion parameters (the initial vertical velocity and the vertical acceleration). The height of the projectile at this peak position can be determined using the equation

y = v_iy • t + 0.5 • g • t²

where v_iy is the initial vertical velocity in m/s, g is the acceleration of gravity (-9.8 m/s/s) and t is the time in seconds it takes to reach the peak. This equation can be successfully used to determine the vertical displacement of the projectile through the first half of its trajectory (i.e., peak height) provided that the algebra is properly performed and the proper values are substituted for the given variables. Special attention should be given to the facts that the t in the equation is the time up to the peak and the g has a negative value of -9.8 m/s/s.

Check Your Understanding

Answer the following questions and click the button to see the answers.

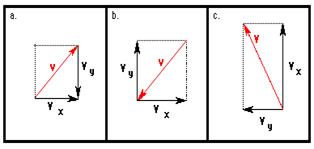
1. Aaron Agin is resolving velocity vectors into horizontal and vertical components. For each case, evaluate whether Aaron’s diagrams are correct or incorrect. If incorrect, explain the problem or make the correction.

See Answer

A: Aaron is wrong. If v is upwards and rightwards then v_y should be directed upwards. Aaron’s is downwards.

B: Aaron is wrong. If v is downwards and leftwards then v_x should be directed leftwards and v_y should be directed downwards. Aaron’s components are in the wrong direction.

C: Aaron is wrong. This is a labeling problem. Aaron has labeled the horizontal component as v_y and the vertical component as v_x.

close

2. Use trigonometric functions to resolve the following velocity vectors into horizontal and vertical components. Then utilize kinematic equations to calculate the other motion parameters. Be careful with the equations; be guided by the principle that “perpendicular components of motion are independent of each other.”

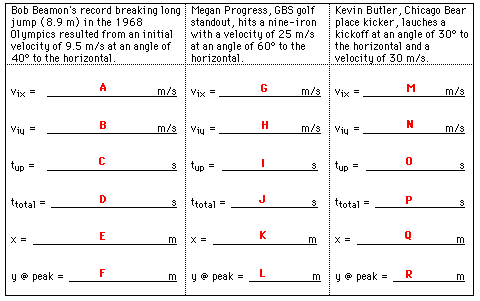See Answer

A: v_ix = 9.5 m/s • cos(40 degrees) = 7.28 m/s

B : v_iy = 9.5 m/s • sin(40 degrees) = 6.11 m/s

C: t_up = (6.11 m/s) / (9.8 m/s/s) = 0.623 s

D: t_total = 2 • (0.623 s) = 1.25 s

E: x = 7.28 m/s • 1.25 s = 9.07 m

F: y = (6.11 m/s) • (0.623 s) + 0.5*(-9.8 m/s/s) • (0.623 s )² = 1.90 m

G: v_ix = 25 m/s • cos (60 degrees) = 12.5 m/s

H: v_iy = 25 m/s • sin (60 degrees) = 21.7 m/s

I: t_up = (21.7 m/s) / (9.8 m/s/s) = 2.21 s

J: t_total = 2 • 2.21 s = 4.42 s

K: x = 12.5 m/s • 4.42 s = 55.2 m

L: y = 21.7 m/s • 2.21 s + 0.5 • (-9.8 m/s/s) • (2.21 s )² = 23.9 m

M: v_ix = 30 m/s • cos (30 degrees) = 26.0 m/s

N: v_iy = 30 m/s • sin (30 degrees) = 15.0 m/s

O: t_up = (15.0 m/s) / (9.8 m/s/s) = 1.53 s

P: t_total = 2 • 1.53 s = 3.06 s

Q: x = 26.0 m/s • 3.06 s = 79.5 m

R: y = 15.0 m/s • 1.53 s + 0.5 • (-9.8 m/s/s) • (1.53 s )² = 11.5 m

3. Utilize kinematic equations and projectile motion concepts to fill in the blanks in the following tables.

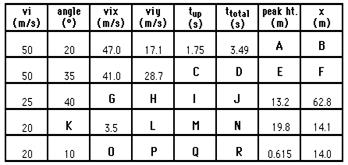
See Answer

A: 14.9 m

B: 164 m

C: 2.93 s

D: 5.85 s

E: 42.0 m

F: 240 m

G: 19.2 m/s

H: 16.1 m/s

I: 1.64 s

J: 3.28 s

K: 79.9 deg

L: 19.7 m/s

M: 2.01 s

N: 4.02 s

O: 19.7 m/s

P: 3.47 m/s

Q: 0.354 s

R: 0.709 s