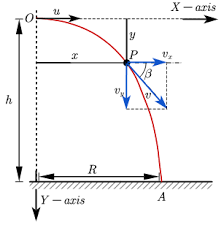
The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions – both horizontally and vertically. Since these two components of motion are independent of each other, two distinctly separate sets of equations are needed – one for the projectile’s horizontal motion and one for its vertical motion. Thus, the three equations above are transformed into two sets of three equations. For the horizontal components of motion, the equations are
x = vix•t + 0.5*ax*t2
vfx = vix + ax•t
vfx2 = vix2 + 2*ax•x
| where | x = horiz. Displacement | ax = horiz. acceleration | t = time |
| vfx = final horiz. velocity | vix = initial horiz. velocity |
Of these three equations, the top equation is the most commonly used. An application of projectile concepts to each of these equations would also lead one to conclude that any term with ax in it would cancel out of the equation since ax = 0 m/s/s. Once this cancellation of ax terms is performed, the only equation of usefulness is:
x = vix•t
Equations for the Vertical Motion of a Projectile
For the vertical components of motion, the three equations are
y = viy•t + 0.5*ay*t2
vfy = viy + ay•t
vfy2 = viy2 + 2*ay•y
| where | y = vert. displacement | ay = vert. acceleration | t = time |
| vfy = final vert. velocity | viy = initial vert. velocity |
In each of the above equations, the vertical acceleration of a projectile is known to be -9.8 m/s/s (the acceleration of gravity). Furthermore, for the special case of the first type of problem (horizontally launched projectile problems), viy = 0 m/s. Thus, any term with viy in it will cancel out of the equation.
The two sets of three equations above are the kinematic equations that will be used to solve projectile motion problems.