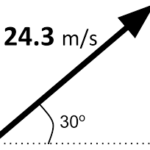
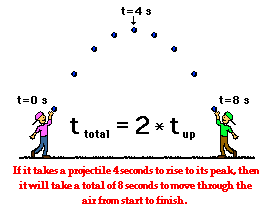The time for a projectile to rise vertically to its peak (as well as the time to fall from the peak) is dependent upon vertical motion parameters. The process of rising vertically to the peak of a trajectory is a vertical motion and is thus dependent upon the initial vertical velocity and the vertical acceleration (g = 9.8 m/s/s, down). The process of determining the time to rise to the peak is an easy process – provided that you have a solid grasp of the concept of acceleration. When first introduced, it was said that acceleration is the rate at which the velocity of an object changes. An acceleration value indicates the amount of velocity change in a given interval of time. To say that a projectile has a vertical acceleration of -9.8 m/s/s is to say that the vertical velocity changes by 9.8 m/s (in the – or downward direction) each second. For example, if a projectile is moving upwards with a velocity of 39.2 m/s at 0 seconds, then its velocity will be 29.4 m/s after 1 second, 19.6 m/s after 2 seconds, 9.8 m/s after 3 seconds, and 0 m/s after 4 seconds. For such a projectile with an initial vertical velocity of 39.2 m/s, it would take 4 seconds for it to reach the peak where its vertical velocity is 0 m/s. With this notion in mind, it is evident that the time for a projectile to rise to its peak is a matter of dividing the vertical component of the initial velocity (viy) by the acceleration of gravity.
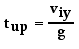
Once the time to rise to the peak of the trajectory is known, the total time of flight can be determined. For a projectile that lands at the same height which it started, the total time of flight is twice the time to rise to the peak. Recall from the last section of Lesson 2 that the trajectory of a projectile is symmetrical about the peak. That is, if it takes 4 seconds to rise to the peak, then it will take 4 seconds to fall from the peak; the total time of flight is 8 seconds. The time of flight of a projectile is twice the time to rise to the peak.