Lesson 2 has thus far focused on how to analyse motion situations using the work and energy relationship. The relationship could be summarized by the following statements:
| There is a relationship between work and mechanical energy change. Whenever work is done upon an object by an external or nonconservative force, there will be a change in the total mechanical energy of the object. If only internal forces are doing work (no work done by external forces), there is no change in total mechanical energy; the total mechanical energy is said to be “conserved.” The quantitative relationship between work and the two forms of mechanical energy is expressed by the following equation:KEi + PEi + Wext = KEf + PEf |
Now an effort will be made to apply this relationship to a variety of motion scenarios in order to test our understanding.
Check Your Understanding
Use your understanding of the work-energy theorem to answer the following questions. Then click the button to view the answers.
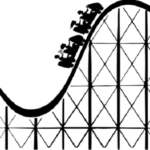
1. Consider the falling and rolling motion of the ball in the following two resistance-free situations. In one situation, the ball falls off the top of the platform to the floor. In the other situation, the ball rolls from the top of the platform along the staircase-like pathway to the floor. For each situation, indicate what types of forces are doing work upon the ball. Indicate whether the energy of the ball is conserved and explain why. Finally, fill in the blanks for the 2-kg ball.
See Answer

The only force doing work is gravity. Since it is an internal or conservative force, the total mechanical energy is conserved. Thus, the 100 J of original mechanical energy is present at each position. So the KE for A is 50 J.
The PE at the same stairstep is 50 J (C) and thus the KE is also 50 J (D).
The PE at zero height is 0 J (F and I). And so the kinetic energy at the bottom of the hill is 100 J (G and J).
Using the equation KE = 0.5*m*v2, the velocity can be determined to be 7.07 m/s for B and E and 10 m/s for H and K.
The answers given here for the speed values are presuming that all the kinetic energy of the ball is in the form of translational kinetic energy. In actuality, some of the kinetic energy would be in the form of rotational kinetic energy. Thus, the actual speed values would be slightly less than those indicated. (Rotational kinetic energy is not discussed here at The Physics Classroom Tutorial.)
2. If frictional forces and air resistance were acting upon the falling ball in #1 would the kinetic energy of the ball just prior to striking the ground be more, less, or equal to the value predicted in #1?
See Answer

The kinetic energy would be less in a situation that involves friction. Friction would do negative work and thus remove mechanical energy from the falling ball.
close
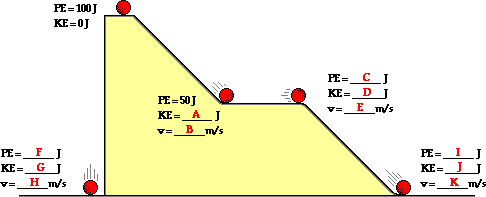
Use the following diagram to answer questions #3 – #5. Neglect the effect of resistance forces.
3. As the object moves from point A to point D across the surface, the sum of its gravitational potential and kinetic energies ____.
| a. decreases, only | b. decreases and then increases |
| c. increases and then decreases | d. remains the same |
See Answer

The answer is D. The total mechanical energy (i.e., the sum of the kinetic and potential energies) is everywhere the same whenever there are no external or nonconservative forces (such as friction or air resistance) doing work.
4. The object will have a minimum gravitational potential energy at point ____.
| a. A | b. B | c. C | d. D | e. E |
See Answer

The answer is B. Gravitational potential energy depends upon height (PE=m*g*h). The PE is a minimum when the height is a minimum. Position B is the lowest position in the diagram.
5. The object’s kinetic energy at point C is less than its kinetic energy at point ____.
| a. A only | b. A, D, and E | c. B only | d. D and E |
See Answer

The answer is C. Since the total mechanical energy is conserved, kinetic energy (and thus, speed) will be greatest when the potential energy is smallest. Point B is the only point that is lower than point C. The reasoning would follow that point B is the point with the smallest PE, the greatest KE, and the greatest speed. Therefore, the object will have less kinetic energy at point C than at point B (only).
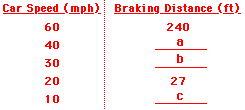
6. Many drivers’ education books provide tables that relate a car’s braking distance to the speed of the car (see table below). Utilize what you have learned about the stopping distance-velocity relationship to complete the table.
See Answer

A: 108 ft
Compare 20 mph to 40 mph – a two-fold increase in speed. A two-fold increase in speed means a four-fold increase in stopping distance. Multiply 27 by 4.
B: 60 ft
Compare 60 mph to 30 mph – a two-fold decrease in speed. A two-fold decrease in speed means a four-fold decrease in stopping distance. Divide 240 by 4.
C: 6.8 ft
Compare 20 mph to 10 mph – a two-fold decrease in speed. A two-fold decrease in speed means a four-fold decrease in stopping distance. Divide 27 by 4.
7. Some driver’s license exams have the following question.
A car moving 50 km/hr skids 15 meters with locked brakes. How far will the car skid with locked brakes if it is moving at 150 km/hr?
See Answer

The car skids 135 m. There is a three-fold increase in the speed of the car (150 / 50 = 3). Thus, there must be a nine-fold increase in the stopping distance. Multiply 15 meters by 9.
8. Two baseballs are fired into a pile of hay. If one has twice the speed of the other, how much farther does the faster baseball penetrate? (Assume that the force of the haystack on the baseballs is constant).
See Answer

The faster baseball penetrates four times as far. When there is a two-fold increase in speed, there is a four-fold increase in stopping distance. For constant resistance forces, stopping distance is proportional to the square of the speed.
9. Use the law of conservation of energy (assume no friction) to fill in the blanks at the various marked positions for a 1000-kg roller coaster car.
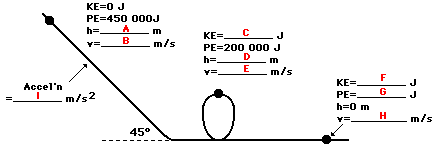
See Answer

A: h = 45.9 m (from 450 000 =1000*9.8*h)
B: v = 0 m/s (since KE = 0 J)
C: KE = 250 000 J (KE + PE must equal 450 000 J)
D: h = 20.4 m (From 200 000 =1000*9.8*h)
E: v = 22.4 m/s (from 250 000 = 0.5*1000*v^2)
F: KE = 450 000 J (KE + PE must equal 450 000 J)
G: PE = 0 J (since the height is 0 m)
H: v = 31.6 m/s (from 500 000 = 0.5*1000*v^2)
I: a = 7.07 m/s/s (since a = g*sin angle)
10. If the angle of the initial drop in the roller coaster diagram above were 60 degrees (and all other factors were kept constant), would the speed at the bottom of the hill be any different? Explain.
See Answer

The angle does not affect the speed at the bottom of the incline. The speed at the bottom of the incline is dependent upon the initial height of the incline. Many students believe that a smaller angle means a smaller speed at the bottom. But such students are confusing speed with acceleration. A smaller angle will lead to a smaller acceleration along the incline.
11. Determine Li Ping Phar’s (a mass of approximately 50 kg) speed at locations B, C, D and E.
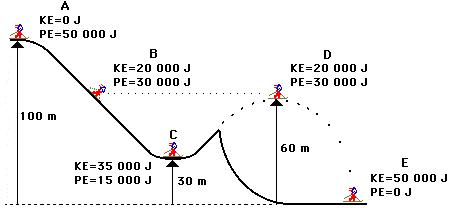
See Answer

B: KE = 0.5 •m • v2
20 000 J = 0.5 • (50 kg) • v2
v = 28.3 m/s
C: KE = (0.5 •m • v2
35 000 J = 0.5 • (50 kg) • v2
v = 37.4 m/s
D: same as postition B
v = 28.3 m/s
E: KE = 0.5 •m • v2
50 000 J = 0.5 • (50 kg) • v2
v = 44.7 m/s
12. An object which weighs 10 N is dropped from rest from a height of 4 meters above the ground. When it has free-fallen 1 meter its total mechanical energy with respect to the ground is ____.
| a. 2.5 J | b. 10 J | c. 30 J | d. 40 J |
See Answer

The answer is D.
Energy is conserved in free-fall situations (no external forces doing work). Thus, the total mechanical energy initially is everywhere the same. Whatever total mechanical energy (TME) it has initially, it will maintain throughout the course of its motion. The object begins with 39.2 J of potential energy (PE = m * g * h = 1 kg * 9.8 m/s/s * 4 m = 39.2 J) and no kinetic energy. The total mechanical energy (KE + PE) is 39.2 J.
Observe that a confusion of mass (1 kg) and weight (9.8 N) will inevitably lead to the wrong answer.
13. During a certain time interval, a 20-N object free-falls 10 meters. The object gains _____ Joules of kinetic energy during this interval.
| a. 10 | b. 20 | c. 200 | d. 2000 |
See Answer

The answer is C.
The total amount of mechanical energy is conserved in free-fall situations (no external forces doing work). Thus, the potential energy that is lost is transformed into kinetic energy. The object loses 200 J of potential energy (PE loss = m * g * h where the m•g is 200 N (i.e., the object’s weight).
Observe that a confusion of mass (~20 kg) and weight (200 N) will inevitably lead to the wrong answer.
14. A rope is attached to a 50.0-kg crate to pull it up a frictionless incline at constant speed to a height of 3-meters. A diagram of the situation and a free-body diagram are shown below. Note that the force of gravity has two components (parallel and perpendicular component); the parallel component balances the applied force and the perpendicular component balances the normal force.
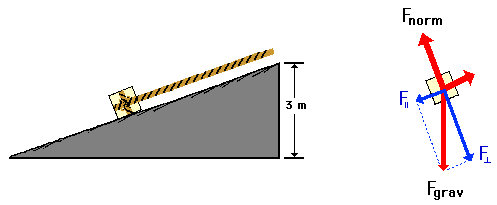
Of the forces acting upon the crate, which one(s) do work upon it?
See Answer

Both gravity and applied forces do work. The normal force does not do work since the angle between Fnorm and the displacement is 90 degrees. (If necessary, review the lesson on work.)
close
Based upon the types of forces acting upon the system and their classification as internal or external forces, is energy conserved? Explain.
See Answer

No!
The applied force is an external or nonconservative force. And since it does work, the total mechanical energy is not conserved.
close
Calculate the amount of work done upon the crate.
See Answer

Wext = 1470 J
Start with TMEi + Wext = TMEf
KEi + PEi + Wext = KEf + PEf
KEi + 0 J + Wext = KEf + (50 kg) * (9.8 m/s/s) * (3 m)
(KEi = KEf since speed is constant. Thus, both KE terms can be eliminated from the equation.)
Wext = (50 kg) * (9.8 m/s/s) * (3 m) = 1470 J