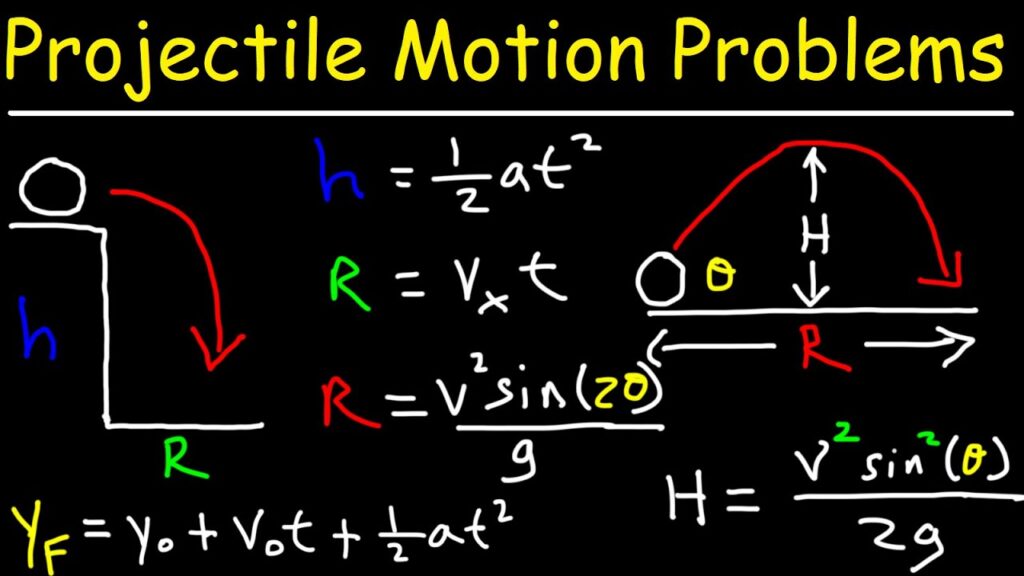
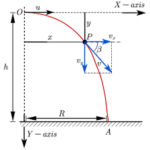
To illustrate the usefulness of the above equations in making predictions about the motion of a projectile, consider the solution to the following problem.

ExampleA pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table’s edge and the ball’s landing location.

The solution of this problem begins by equating the known or given values with the symbols of the kinematic equations – x, y, v_ix, v_iy, a_x, a_y, and t. Because horizontal and vertical information is used separately, it is a wise idea to organized the given information in two columns – one column for horizontal information and one column for vertical information. In this case, the following information is either given or implied in the problem statement:

                                                                                                        

Horizontal Information	Vertical Information
x = ???vix = 2.4 m/sax = 0 m/s/s	y = -0.60 mviy = 0 m/say = -9.8 m/s/s

As indicated in the table, the unknown quantity is the horizontal displacement (and the time of flight) of the pool ball. The solution of the problem now requires the selection of an appropriate strategy for using the kinematic equations and the known information to solve for the unknown quantities. It will almost always be the case that such a strategy demands that one of the vertical equations be used to determine the time of flight of the projectile and then one of the horizontal equations be used to find the other unknown quantities (or vice versa – first use the horizontal and then the vertical equation). An organized listing of known quantities (as in the table above) provides cues for the selection of the strategy. For example, the table above reveals that there are three quantities known about the vertical motion of the pool ball. Since each equation has four variables in it, knowledge of three of the variables allows one to calculate a fourth variable. Thus, it would be reasonable that a vertical equation is used with the vertical values to determine time and then the horizontal equations be used to determine the horizontal displacement (x). The first vertical equation (y = v_iy•t +0.5•a_y•t²) will allow for the determination of the time. Once the appropriate equation has been selected, the physics problem becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

-0.60 m = (0 m/s)•t + 0.5•(-9.8 m/s/s)•t²

Since the first term on the right side of the equation reduces to 0, the equation can be simplified to

-0.60 m = (-4.9 m/s/s)•t²

If both sides of the equation are divided by -5.0 m/s/s, the equation becomes

0.122 s² = t²

By taking the square root of both sides of the equation, the time of flight can then be determined.

t = 0.350 s (rounded from 0.3499 s)

Once the time has been determined, a horizontal equation can be used to determine the horizontal displacement of the pool ball. Recall from the given information, v_ix = 2.4 m/s and a_x = 0 m/s/s. The first horizontal equation (x = v_ix•t + 0.5•a_x•t²) can then be used to solve for “x.” With the equation selected, the physics problem once more becomes transformed into an algebra problem. By substitution of known values, the equation takes the form of

x = (2.4 m/s)•(0.3499 s) + 0.5•(0 m/s/s)•(0.3499 s)²

Since the second term on the right side of the equation reduces to 0, the equation can then be simplified to

x = (2.4 m/s)•(0.3499 s)

Thus,

x = 0.84 m (rounded from 0.8398 m)

The answer to the stated problem is that the pool ball is in the air for 0.35 seconds and lands a horizontal distance of 0.84 m from the edge of the pool table.

 

The following procedure summarizes the above problem-solving approach.

1.      Carefully read the problem and list known and unknown information in terms of the symbols of the kinematic equations. For convenience sake, make a table with horizontal information on one side and vertical information on the other side.

2.      Identify the unknown quantity that the problem requests you to solve for.

3.      Select either a horizontal or vertical equation to solve for the time of flight of the projectile.

4.      With the time determined, use one of the other equations to solve for the unknown. (Usually, if a horizontal equation is used to solve for time, then a vertical equation can be used to solve for the final unknown quantity.)

One caution is in order. The sole reliance upon 4- and 5-step procedures to solve physics problems is always a dangerous approach. Physics problems are usually just that – problems! While problems can often be simplified by the use of short procedures as the one above, not all problems can be solved with the above procedure. While steps 1 and 2 above are critical to your success in solving horizontally launched projectile problems, there will always be a problem that doesn’t fit the mold. Problem solving is not like cooking; it is not a mere matter of following a recipe. Rather, problem solving requires careful reading, a firm grasp of conceptual physics, critical thought and analysis, and lots of disciplined practice. Never divorce conceptual understanding and critical thinking from your approach to solving problems.

 

Check Your Understanding

A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

See Answer

Horizontal Info:	Vertical Info:
x = 35.0 m	y = -22.0 m
vix = ???	viy = 0 m/s
ax = 0 m/s/s	ay = -9.8 m/s/s

Use y = v_iy• t + 0.5 • a_y • t² to solve for time; the time of flight is 2.12 seconds.

Now use x = v_ix• t + 0.5 • a_x• t² to solve for v_ix

Note that a_x is 0 m/s/s so the last term on the right side of the equation cancels. By substituting 35.0 m for x and 2.12 s for t, the v_ix can be found to be16.5 m/s.