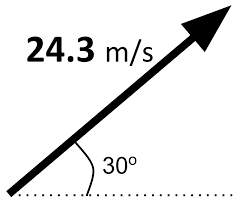
Earlier in this unit, the method of vector resolution was discussed. Vector resolution is the method of taking a single vector at an angle and separating it into two perpendicular parts. The two parts of a vector are known as components and describe the influence of that vector in a single direction. If a projectile is launched at an angle to the horizontal, then the initial velocity of the projectile has both a horizontal and a vertical component. The horizontal velocity component (vx) describes the influence of the velocity in displacing the projectile horizontally. The vertical velocity component (vy) describes the influence of the velocity in displacing the projectile vertically. Thus, the analysis of projectile motion problems begins by using the trigonometric methods discussed earlier to determine the horizontal and vertical components of the initial velocity.
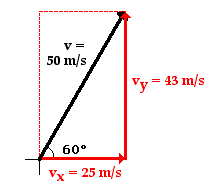Consider a projectile launched with an initial velocity of 50 m/s at an angle of 60 degrees above the horizontal. Such a projectile begins its motion with a horizontal velocity of 25 m/s and a vertical velocity of 43 m/s. These are known as the horizontal and vertical components of the initial velocity. These numerical values were determined by constructing a sketch of the velocity vector with the given direction and then using trigonometric functions to determine the sides of the velocity triangle. The sketch is shown at the right and the use of trigonometric functions to determine the magnitudes is shown below. (If necessary, review this method on an earlier page in this unit.)
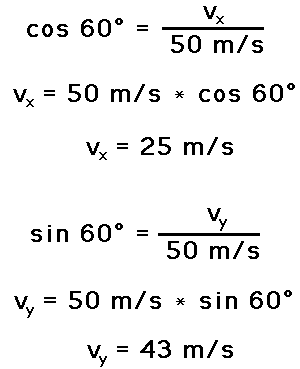
All vector resolution problems can be solved in a similar manner. As a test of your understanding, utilize trigonometric functions to determine the horizontal and vertical components of the following initial velocity values. When finished, click the button to check your answers.
Practice A: A water balloon is launched with a speed of 40 m/s at an angle of 60 degrees to the horizontal.
See Answer
cos (60 deg) = vx / (40 m/s)
vx = 40 m/s • cos (60 deg) = 20.0 m/s
sin (60 deg) = vy/ (40 m/s)
vy = 40 m/s • sin (60 deg) = 34.6 m/s
cos (60 deg) = vx / (40 m/s)
vx = 40 m/s • cos (60 deg) = 20.0 m/s
sin (60 deg) = vy/ (40 m/s)
vy = 40 m/s • sin (60 deg) = 34.6 m/s
Practice B: A motorcycle stunt person traveling 70 mi/hr jumps off a ramp at an angle of 35 degrees to the horizontal.
See Answer
cos (35 deg) = vx / (70 mi/hr)
vx = 70 mi/hr • cos (35 deg) = 57.3 mi/hr
sin (35 deg) = vy / (70 mi/hr)
vy = 70 mi/hr • sin (35 deg) = 40.1 mi/hr
Practice C: A springboard diver jumps with a velocity of 10 m/s at an angle of 80 degrees to the horizontal.
See A
Practice C:
cos (80 deg) = vx / (10 m/s)
vx = 10 m/s • cos (80 deg) = 1.7 m/s
sin (80 deg) = vy / (10 m/s)
vy = 10 m/s • sin (80 deg) = 9.8 m/s
Answer
As mentioned above, the point of resolving an initial velocity vector into its two components is to use the values of these two components to analyze a projectile’s motion and determine such parameters as the horizontal displacement, the vertical displacement, the final vertical velocity, the time to reach the peak of the trajectory, the time to fall to the ground, etc. This process is demonstrated on the remainder of this page. We will begin with the determination of the time.
