The magnitude and direction of the sum of two or more vectors can also be determined by use of an accurately drawn scaled vector diagram. Using a scaled diagram, the head-to-tail method is employed to determine the vector sum or resultant. A common Physics lab involves a vector walk. Either using centimeter-sized displacements upon a map or meter-sized displacements in a large open area, a student makes several consecutive displacements beginning from a designated starting position. Suppose that you were given a map of your local area and a set of 18 directions to follow. Starting at home base, these 18 displacement vectors could be added together in consecutive fashion to determine the result of adding the set of 18 directions. Perhaps the first vector is measured 5 cm, East. Where this measurement ended, the next measurement would begin. The process would be repeated for all 18 directions. Each time one measurement ended, the next measurement would begin. In essence, you would be using the head-to-tail method of vector addition.
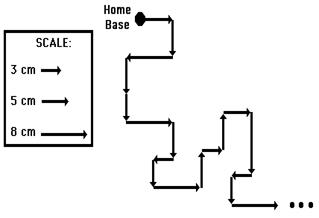
The head-to-tail method involves drawing a vector to scale on a sheet of paper beginning at a designated starting position. Where the head of this first vector ends, the tail of the second vector begins (thus, head-to-tail method). The process is repeated for all vectors that are being added. Once all the vectors have been added head-to-tail, the resultant is then drawn from the tail of the first vector to the head of the last vector; i.e., from start to finish. Once the resultant is drawn, its length can be measured and converted toreal units using the given scale. The direction of the resultant can be determined by using a protractor and measuring its counterclockwise angle of rotation from due East.
A step-by-step method for applying the head-to-tail method to determine the sum of two or more vectors is given below.
1. Choose a scale and indicate it on a sheet of paper. The best choice of scale is one that will result in a diagram that is as large as possible, yet fits on the sheet of paper.
2. Pick a starting location and draw the first vector to scalein the indicated direction. Label the magnitude and direction of the scale on the diagram (e.g., SCALE: 1 cm = 20 m).
3. Starting from where the head of the first vector ends, draw the second vector to scale in the indicated direction. Label the magnitude and direction of this vector on the diagram.
4. Repeat steps 2 and 3 for all vectors that are to be added
5. Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector asResultant or simply R.
6. Using a ruler, measure the length of the resultant and determine its magnitude by converting to real units using the scale (4.4 cm x 20 m/1 cm = 88 m).
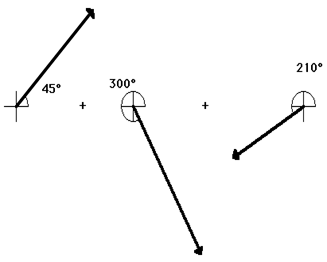
7. Measure the direction of the resultant using the counterclockwise convention discussed earlier in this lesson.
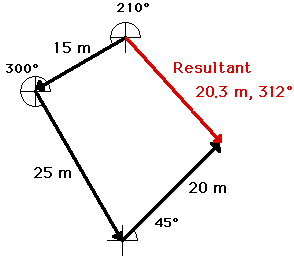
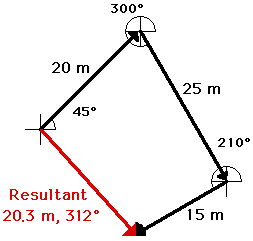
An example of the use of the head-to-tail method is illustrated below. The problem involves the addition of three vectors:
20 m, 45 deg. + 25 m, 300 deg. + 15 m, 210 deg.
SCALE: 1 cm = 5 m
The head-to-tail method is employed as described above and the resultant is determined (drawn in red). Its magnitude and direction is labeled on the diagram.
SCALE: 1 cm = 5 m
Interestingly enough, the order in which three vectors are added has no effect upon either the magnitude or the direction of the resultant. The resultant will still have the same magnitude and direction. For example, consider the addition of the same three vectors in a different order.
15 m, 210 deg. + 25 m, 300 deg. + 20 m, 45 deg.
SCALE: 1 cm = 5 m
When added together in this different order, these same three vectors still produce a resultant with the same magnitude and direction as before (20. m, 312 degrees). The order in which vectors are added using the head-to-tail method is insignificant.
SCALE: 1 cm = 5 m