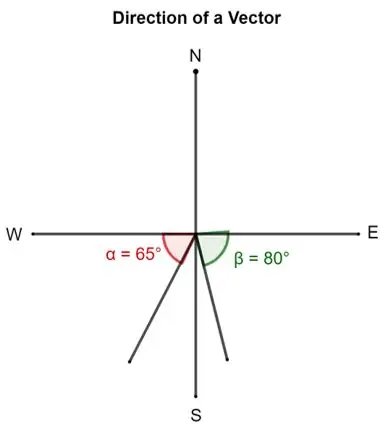
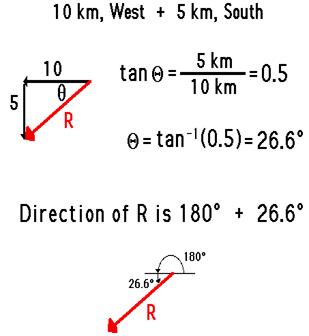
The measure of an angle as determined through use of SOH CAH TOA is not always the direction of the vector. The following vector addition diagram is an example of such a situation. Observe that the angle within the triangle is determined to be 26.6 degrees using SOH CAH TOA. This angle is the southward angle of rotation that the vector R makes with respect to West. Yet the direction of the vector as expressed with the CCW (counterclockwise from East) convention is 206.6 degrees.

 

                                                                                 

Test your understanding of the use of SOH CAH TOA to determine the vector direction by trying the following two practice problems. In each case, use SOH CAH TOA to determine the direction of the resultant. When finished, click the button to view the answer.

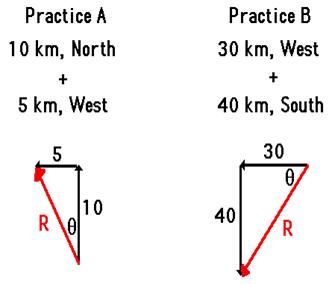
See Answer to Practice A

tan(Theta) = (5/10) = 0.5

Theta = tan^-1 (0.5)

Theta = 26.6 degrees

Direction of R = 90 deg + 26.6 deg

Direction of R = 116.6 deg

See Answer to Practice B

tan(Theta) = (40/30) = 1.333

Theta = tan^-1 (1.333)

Theta = 53.1 degrees

Direction of R = 180 deg + 53.1 deg

Direction of R = 233.1 deg

In the above problems, the magnitude and direction of the sum of two vectors is determined using the Pythagorean theorem and trigonometric methods (SOH CAH TOA). The procedure is restricted to the addition of two vectors that make right angles to each other. When the two vectors that are to be added do not make right angles to one another, or when there are more than two vectors to add together, we will employ a method known as the head-to-tail vector addition method. This method is described below.