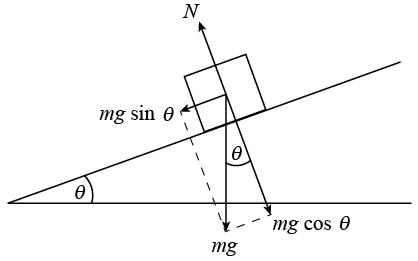
It was learned in the previous part of this lesson that a free-falling object is an object that is falling under the sole influence of gravity. A free-falling object has an acceleration of 9.8 m/s/s, downward (on Earth). This numerical value for the acceleration of a free-falling object is such an important value that it is given a special name. It is known as the acceleration of gravity – the acceleration for any object moving under the sole influence of gravity. A matter of fact, this quantity known as the acceleration of gravity is such an important quantity that physicists have a special symbol to denote it – the symbol g. The numerical value for the acceleration of gravity is most accurately known as 9.8 m/s/s. There are slight variations in this numerical value (to the second decimal place) that are dependent primarily upon on altitude. We will occasionally use the approximated value of 10 m/s/s in The Physics Classroom Tutorial in order to reduce the complexity of the many mathematical tasks that we will perform with this number. By so doing, we will be able to better focus on the conceptual nature of physics without too much of a sacrifice in numerical accuracy.
g = 9.8 m/s/s, downward
( ~ 10 m/s/s, downward)
Look It Up!
| The value of the acceleration of gravity (g) is different in different gravitational environments. |
Investigate!
Even on the surface of the Earth, there are local variations in the value of the acceleration of gravity (g). These variations are due to latitude, altitude and the local geological structure of the region.
Recall from an earlier lesson that acceleration is the rate at which an object changes its velocity. It is the ratio of velocity change to time between any two points in an object’s path. To accelerate at 9.8 m/s/s means to change the velocity by 9.8 m/s each second.
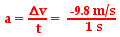
If the velocity and time for a free-falling object being dropped from a position of rest were tabulated, then one would note the following pattern.
| Time (s) | Velocity (m/s) |
| 0 | 0 |
| 1 | – 9.8 |
| 2 | – 19.6 |
| 3 | – 29.4 |
| 4 | – 39.2 |
| 5 | – 49.0 |
Observe that the velocity-time data above reveal that the object’s velocity is changing by 9.8 m/s each consecutive second. That is, the free-falling object has an acceleration of approximately 9.8 m/s/s.
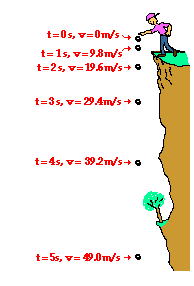 Another way to represent this acceleration of 9.8 m/s/s is to add numbers to our dot diagram that we saw earlier in this lesson. The velocity of the ball is seen to increase as depicted in the diagram at the right. (NOTE: The diagram is not drawn to scale – in two seconds, the object would drop considerably further than the distance from shoulder to toes.)
Another way to represent this acceleration of 9.8 m/s/s is to add numbers to our dot diagram that we saw earlier in this lesson. The velocity of the ball is seen to increase as depicted in the diagram at the right. (NOTE: The diagram is not drawn to scale – in two seconds, the object would drop considerably further than the distance from shoulder to toes.)