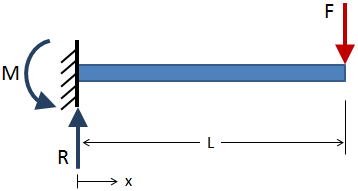
Shear Force

This result means that an abrupt change in the shear force occurs at any point where a concentrated load acts.

The shear force does not change at the point of application of a couple

Bending Moment

1. The bending moment does not change as we pass through the point of application of a concentrated load.

2. At the point of application of a concentrated load P, the rate of change dM/dx of the bending moment decreases abruptly by an amount equal to P.

The bending moment changes abruptly at the point of application of a couple.

Note: If the sign convention for the distributed load is reversed, so that q is positive upward instead of downward, then the minus sign is omitted in the preceding equation.

5)      

b)      The difference in shear values between any two points on the shear diagram is equal to the (-) area under the distributed load curve between those same two points

This equation is valid only when distributed loads act on the beam between points ‘A’ and ‘B’, but not when a concentrated load is acting between point ‘A’ and ‘B’

c)      The ordinate on the shear diagram (V) is equal to the slope on the bending moment diagram

d)      The difference in values between any two points on the moment diagram is equal to the area under the shear diagram between those same two points

This equation is valid even when concentrated loads act on the beam between points ‘A’ and ‘B’, but not when a couple is acting between point ‘A’ and ‘B’

e)      At those points at which the shear curve crosses the reference axis (i.e., V=0), the value of the moment on the moment diagram is a local maximum or minimum.

f)       The ordinate on the axial force diagram (N) is equal to zero at an axial force release; the ordinate on the shear diagram (V) is zero at a shear release; and the ordinate on the moment diagram (M) is zero at a moment release.

7)      If the bending moments at both ends of a beam are zero, as is usually the case with a simple beam, then the area of the shear-force diagram between the ends of the beam must be zero provided no couples act on the beam

8)      The maximum positive and negative bending moments in a beam may occur at the following places

a)      A cross section where a concentrated load is applied and the shear force changes sign

b)      A cross section where the shear force equals zero

c)      A point of support where a vertical reaction is present, and

d)      A cross section where a couple is applied.

1)      The deflection of the beam at any point along its axis is the displacement of that point from its original position, measured in the y direction.