a)      

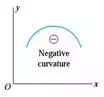
i)        Curvature is a measure of how sharply a beam is bent

ii)      If the load on a beam is small, the beam will be nearly straight, the radius of curvature will be very large, and the curvature will be very small and vice versa.

iii)    Under these special conditions of small deflections, the equation for the curvature becomes

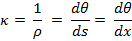
c)      

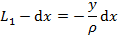
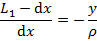
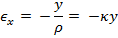
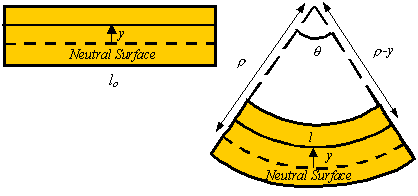
i)        Longitudinal strains in the beam are proportional to the curvature and vary linearly with the distance y from the neutral surface regardless of the shape of the stress-strain curve of the material i.e. properties of material. When the point under consideration is above the neutral surface, the distance y is positive.

ii)      The normal strain in a beam was derived solely from the geometry of the deformed beam—the properties of the material did not enter into the discussion.

e)      The longitudinal strains in a beam are accompanied by transverse strains (that is, normal strains in the y and z directions) because of the effects of Poisson’s ratio. However, there are no accompanying transverse stresses because beams are free to deform laterally. This stress condition is analogous to that of a prismatic bar in tension or compression, and therefore longitudinal elements in a beam in pure bending are in a state of uniaxial stress.