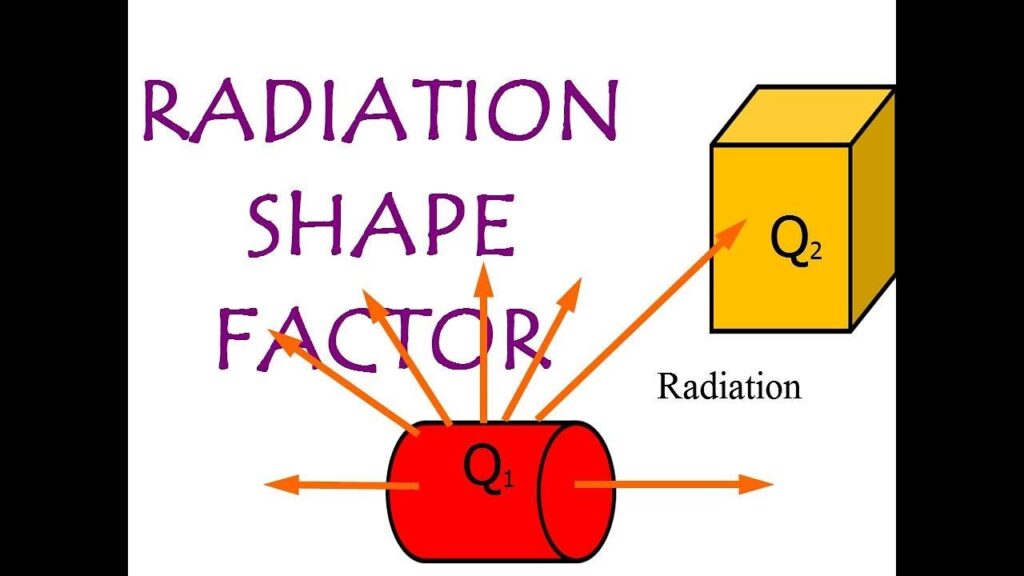
1) Radiation heat transfer between surfaces depends on the orientation of the surfaces relative to each other as well as their radiation properties and temperatures
2) To account for the effects of orientation on radiation heat transfer between two surfaces, we define a new parameter called the view factor, which is a purely geometric quantity and is independent of the surface properties and temperature.
a) It is also called the shape factor, configuration factor, and angle factor.
b) The view factor based on the assumption that the surfaces are diffuse emitters and diffuse reflectors is called the diffuse view factor, and the view factor based on the assumption that the surfaces are diffuse emitters but specular reflectors is called the specular view factor.
3) The view factor from a surface i to a surface j is denoted by Fi → j or Fij and is defined as
Fij = the fraction of the radiation leaving surface i that strikes surface j directly
a) The view factor F12 represents the fraction of radiation leaving surface 1 that strikes surface 2 directly, and F21 represents the fraction of the radiation leaving surface 2 that strikes surface 1 directly.
b) Radiation that strikes a surface does not need to be absorbed by that surface
c) Radiation that strikes a surface after being reflected by other surfaces is not considered in the evaluation of view factors.
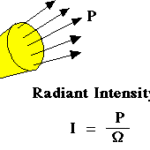
4) Surface 1 emits and reflects radiation diffusely in all directions with a constant intensity of
, and the solid angle subtended by when viewed by is.
a) in the direction of is. Noting that , the portion of this radiation that strikes is
b) The total rate at which radiation leaves (via emission and reflection) in all directions is the radiosity (which is) times the surface area is
c) differential view factor becomes
5) VIEW FACTOR RELATIONS
a) Radiation analysis on an enclosure consisting of N surfaces requires the evaluation of N2 view factors it is neither practical nor necessary to evaluate all of the view factors directly. Once few shape factors are known we use certain fundamental relations to find others
i) The Reciprocity Relation:
ii) The Summation Rule:
(1) When formulating a radiation problem, we usually form an enclosure consisting of the surfaces interacting radiatively. Even openings are treated as imaginary surfaces with radiation properties equivalent to those of the opening.
(2) The conservation of energy principle requires that the entire radiation leaving any surface i of an enclosure be intercepted by the surfaces of the enclosure. Therefore, the sum of the view factors from surface i of an enclosure to all surfaces of the enclosure, including to itself, must equal unity.
Applying the summation rule to surface 1 of a three-surface enclosure yields
iii) The Superposition Rule:
(1)
iv) The Symmetry Rule
(1) The symmetry rule can be expressed as two (or more) surfaces that possess symmetry about a third surface will have identical view factors from that surface i.e. if the surfaces j and k are symmetric about the surface i then
Comments are closed.