1)      

b)      In general, the differential solid angle dω subtended by a differential surface area dA when viewed from a point at a distance r from dA is expressed as

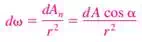
Where α is the angle between the normal of the surface and the direction of viewing

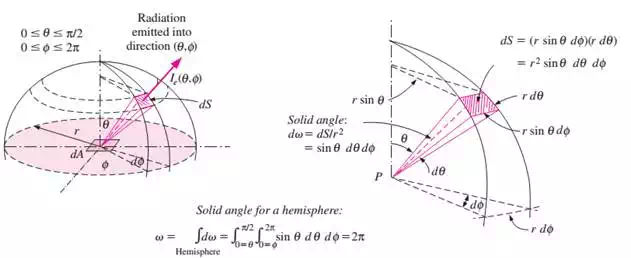
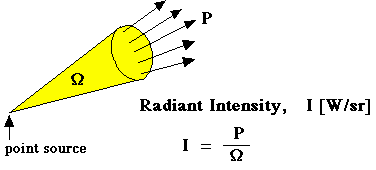
4)    Intensity of Emitted Radiation

a)      The radiation intensity for emitted radiation  is defined as the rate at which radiation energy is emitted in the direction per unit area normal to this direction and per unit solid angle about this direction

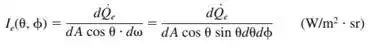
b)      The radiation flux for emitted radiation is the emissive power E (the rate at which radiation energy is emitted per unit area of the emitting surface), which can be expressed in differential form as

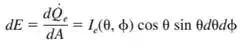
c)      Noting that the hemisphere above the surface will intercept all the radiation rays emitted by the surface, the emissive power from the surface into the hemisphere surrounding it can be determined by integration

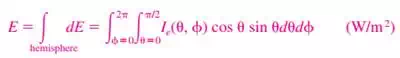
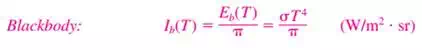
5)    Incident Radiation

a)      The radiation intensity for incident radiation  is defined as the rate at which radiation energy is incident from the direction per unit area of the receiving surface normal to this direction and per unit solid angle about this direction. Here  is the angle between the direction of incident radiation and the normal of the surface

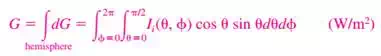
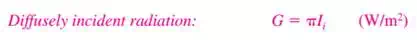
6)    Radiosity

a)      Surfaces emit radiation as well as reflecting it, and thus the radiation leaving a surface consists of emitted and reflected components

b)      The rate at which radiation energy leaves (emitted + reflected) a unit area of a surface in all directions. This quantity is called the Radiosity J

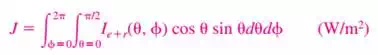
c)      For a blackbody, radiosity J is equivalent to the emissive power  since a blackbody absorbs the entire radiation incident on it and there is no reflected component in radiosity.

7)    Spectral Quantities

a)      Sometimes it is necessary to consider the variation of radiation with wavelength as well as direction, and to express quantities at a certain wavelength  or per unit wavelength interval about. Such quantities are referred to as spectral quantities to draw attention to wavelength dependence

b)      The spectral radiation intensity for example, is simply the total radiation  intensity per unit wavelength interval about.

c)      The radiation intensity for emitted radiation  is defined as the rate at which radiation energy is emitted at a wavelength  in the direction per unit area normal to this direction and per unit solid angle about this direction

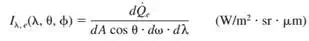
d)      Spectral emissive power

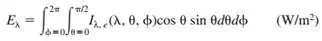
e)      Similar relations can be obtained for spectral irradiation, and spectral radiosity  by replacing  in this equation by and, respectively.

8)      RADIATIVE PROPERTIES

a)      Most materials encountered in practice, such as metals, wood, and bricks are opaque to thermal radiation, and radiation is considered to be a surface phenomenon for such materials. That is, thermal radiation is emitted or absorbed within the first few microns of the surface, and thus we speak of radiative properties of surfaces for opaque materials.

b)      Radiation through such semitransparent materials obviously cannot be considered to be a surface phenomenon since the entire volume of the material interacts with radiation.

c)      On the other hand, both glass and water are practically opaque to infrared radiation.

d)      Materials can exhibit different behavior at different wavelengths, and the dependence on wavelength is an important consideration in the study of radiative properties such as emissivity, absorptivity, reflectivity, and transmissivity of materials.

e)      Emissivity: The emissivity of a surface represents the ratio of the radiation emitted by the surface at a given temperature to the radiation emitted by a blackbody at the same temperature.

i)        The emissivity of a surface is denoted by ε, and 0≤ε ≤1. Emissivity is a measure of how closely a surface approximates a blackbody, for which ε =1.

ii)      It is not constant

iii)    It varies with the temperature of the surface as well as the wavelength and the direction of the emitted radiation.

Spectral directional emissivity	Total directional emissivity	Spectral hemispherical emissivity	Total hemispherical emissivity

f)       

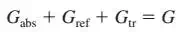
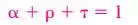
	Spectraldirectional	Spectralhemispherical	Average
Absorptivityα
Reflectivityρ
Transmissivityτ

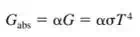
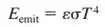
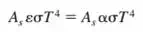
10)           The Greenhouse Effect

a)      Glass has a transparent window in the wavelength range 0.3 μm≤ λ ≤3 μm in which over 90 percent of solar radiation is emitted. On the other hand, the entire radiation emitted by surfaces at room temperature falls in the infrared region. Glass allows the solar radiation to enter but does not allow the infrared radiation from the interior surfaces to escape. This causes a rise in the interior temperature as a result of the energy build-up in the car. This heating effect, which is due to the non-gray characteristic of glass (or clear plastics), is known as the greenhouse effect