Motion of a body vertically downward:

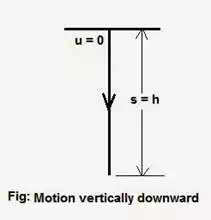
 When a body is releasedfrom rest at a certain height h, then equation of motion are reduced to

            v = gt

            h = ½gt²

            v² = 2gh

Here, u = 0, s = h, a = +g.

[The equations of motion are:

v = u + at,

 s = ut + ½at²,

  v² = u² +2as.

Where, u = initial velocity

             v = Final velocity

             s = Distance Covered

            a = Acceleration

            g = Acceleration due to gravity.]

If any of three quantities t, h and v is given, then other two quantities can be determined.

Motion of a body vertically upward:

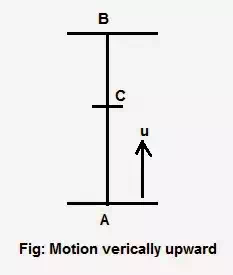
 Suppose a body is projected vertically upward from a point ‘A’ with an initial velocity ‘u’.

1. At time ‘t’, velocity of body is, v = u – gt.    [Here, a = -g]

2. At time ‘t’, the displacement of body with respect to initial position is            s = ut – ½gt²

3. The velocity of a body, when it has a displacement ‘s’ is given by,

            v² = u² – 2gs.

4. When it reaches maximum height from ‘A’, velocity, v = 0

            Then, 0 = u – gt

                                                             Or, t = u/g at point B.

5. Maximum height attained by the body, h = u²/2g

   [Since, v² = u² – 2as, or, 0 = u² – 2gh, or, h = u²/2g]

6. Because displacement s = 0 at the point of projection. Hence

            s = ut – ½gt², or, 0 = ut – ½gt², or, t = 2u/g.

Therefore, Time of ascent = u/g

And, Time of descent = 2u/g – u/g = u/g.

7. At any point ‘C’, between ‘A’ & ‘B’, where AC = s, the velocity ‘v’ is given by,

            v = ± √(u² – 2gs)

This velocity of body whole crossing point ‘C’, upward is +√(u² – 2gs) and while crossing ‘C’ downward is -√(u² – 2gs). The magnitude of velocity will remain same.

8. As, u = √2gh, hence time taken to move up to highest point is also

                        u/g = √2gh/g = √(2h/g).

Motion on an inclined plane:

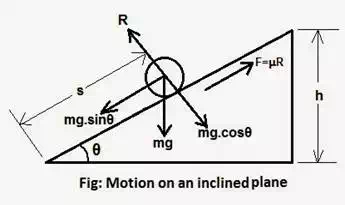
●      1. Here, u = 0, a = g sinθ

Therefore, v = g sinθ × t                             [Since v = u +at]

                  s = ½ (g sinθ × t²)             [Since, s= ut + ½at²]

                 v² = 2 g sinθ × s.                        [Since, v² = u² +2as]

●      2. If ‘s’ is given, then, t² = 2s/(g sinθ).

Note: In the first ½ time, the body moves ¼th of the total distance, which in next half, it moves ¾th of the total distance on an inclined plane.

●      3. Time taken to move down on inclined plane:

            s = ½ g sinθ t²            or, t = √(2s/g sinθ)

            As, h/s = sinθ            or, s = h/sinθ

                        Hence, t = 1/sinθ × √(2h/g)

●      4. Because, v² = 2 g sinθ.s          and, s = h/sinθ

            Hence, v² = 2g sinθ × h/sinθ = 2gh

           Or, v =√(2gh).

●      5. If friction is also present, but motion is taking along the inclined plane, then

            F = ma = mg sinθ – µR

            Or, F = mg sinθ – µmg cosθ.

Or, ma = m (g sinθ – µg cosθ)         or, a = g (sinθ – µ cosθ) = g’

Therefore, v = √(2g’h)

          And, t = 1/sinθ × √(2h/g’).