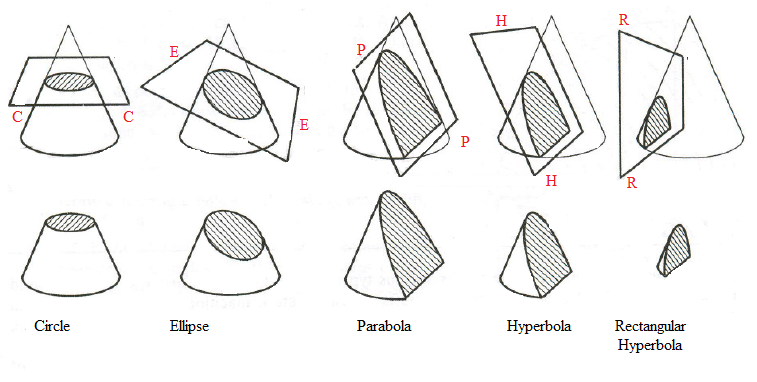
Problem -1, Engineering Curves – Draw Ellipse, Parabola and a Hyperbola on the same axis and same directrix. Take distance of focus from the directrix equal to 50 mm and eccentricity ratio for the ellipse, parabola and hyperbola as 2/3, 1 and 3/2 respectively. Plot at least 8 points. Take suitable point on each curve and draw tangent and normal to the curve at that point.

Procedure: Ellipse
Step-1 First draw a vertical line and horizontal line of convenient length. The vertical line is the directrix and the horizontal line is the axis.
Step-2 Mark a point F, Which is the focus point, at the given distance, that is 50 mm from directrix on axis.
Step-3 Divide the distance of 50 mm into 5 equal divisions.
Step-4 Give the numbers 1,2,3 etc. up to 6 on the right hand side of the focus point F on the axis as shown into the figure. And draw vertical lines parallel to the directrix.
Step-5 For the ellipse the ratio of eccentricity is 2/3, so mark a point Ve, which is vertex of ellipse at the distance of 2 units that is 20 mm from F on the left side as per the figure given above.
Step-6 From Ve draw a vertical line and draw an arc with Ve as center and radius equal to VeF, which will intersect with vertical line drawn from the point Ve.
Step-7 Draw a straight line emerging from the point O and passing from the intersection of the vertical line and the arc drawn previously.
Step-8 Cut the vertical lines emerging from the points 1,2,3, etc. from horizontal axis with the point F as center and radii equal to the distance between the intersection of the respective vertical lines and the inclined line emerging from the point O on both side of the axis as shown into the figure.
Step-9 Give the notations p1, p2, p3 etc. & p1’, p2’, p3’ etc. on both sides as given into the figure.
Step-10 Draw a smooth medium dark free hand curve passing through the points p1, p2, p3 etc. & p1’, p2’, p3’ etc. and the point Ve, which is the curve of an Ellipse.
Procedure: Hyperbola
Step-1 The eccentricity ration of the Hyperbola is 3/2, so mark a point Vh at a distance 3 units, that is 30 mm from the focus point F on the left hand side.
Step-2 From Vh draw a vertical line and draw an arc with Vh as center and radius equal to VhF, which will intersect with vertical line drawn from the point Vh.
Step-3 Draw a straight line emerging from the point O and passing from the intersection of the vertical line and the arc drawn previously.
Step-4 Cut the vertical lines emerging from the points 1,2,3, etc. from horizontal axis with the point F as center and radii equal to the distance between the intersection of the respective vertical lines and the inclined line emerging from the point O on both side of the axis as shown into the figure.
Step-5 Give the notations r1, r2, r3 etc. & r1’, r2’, r3’ etc. on both sides as given into the figure.
Step-6 Draw a smooth medium dark free hand curve passing through the points r1, r2, r3 etc. & r1’, r2’, r3’ etc. and the point Vh, which is the curve of a Hyperbola.
Procedure: Parabola
Step-1 The eccentricity ration of the Parabola is 1, so mark a point Vp at a distance 2.5 units, that is 25 mm from the focus point F on the left hand side.
Step-2 Take the distance from O as O1, O2, O3 etc. on horizontal axis and with F as center cut the lines 1,2,3 etc. respectively, which are perpendicular to the axis and give the notations q1,q2,q3 & q1’, q2’, q3’etc. as shown into the figure.
Step-3 Draw a smooth medium dark free hand curve passing through the points q1,q2,q3 & q1’, q2’, q3’etc. and the point Vp, which is the curve of a Parabola.
Step-4 To draw normal and tangent to of the above curves, mark a point say N on the parabola, from this point N draw a line connecting to the point F, draw a line which is perpendicular to the line FN and intersecting with the directrix, now draw a medium dark line starting from this point and passing through the point N which is Tangent of the curve. And draw a perpendicular line to this tangent and passing through the point N which is normal of the curve. Like in this way the normal and tangent to the Ellipse and Hyperbola are obtained.
Note: Tangent and Normal are perpendicular to each other, so by drawing any one first the other is obtained at perpendicular to the previous one.
Step-5 Give the dimensions by any one method of dimensions and give the name of the components by leader lines wherever necessary.