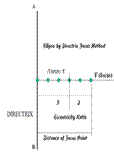
Point F Is 50 mm from a Directrix AB. A Point P is moving in a plane such that the ratio of its distances from F and line AB remains constant and equals to 2/3. Draw locus of point P {Take eccentricity equal to 2/3}.
OR
Draw an Ellipse by Directrix-Focus Method. Take distance of focus as 50 mm from directrix and eccentricity ratio for ellipse as 2/3.
Procedure:
1. Draw a vertical line (Directrix) AB and a horizontal line (Vertex) from approx mid of vertical line. Take focus point F 50 mm from directrix on vertex.
[Alert_Box] Note: Value of Eccentricity Ration gives idea about how the distance of focus point from directrix can be divided. For example Distance of focus point F from directrix is 70 and Eccentricity Ration is given as ¾ then we need to make 30 mm by 40 mm equal parts of 70 mm distance. [/Alert_Box]
2. Divide 50 mm distance in 5 parts (10 mm each) because eccentricity ratio is given in data is 2/3.
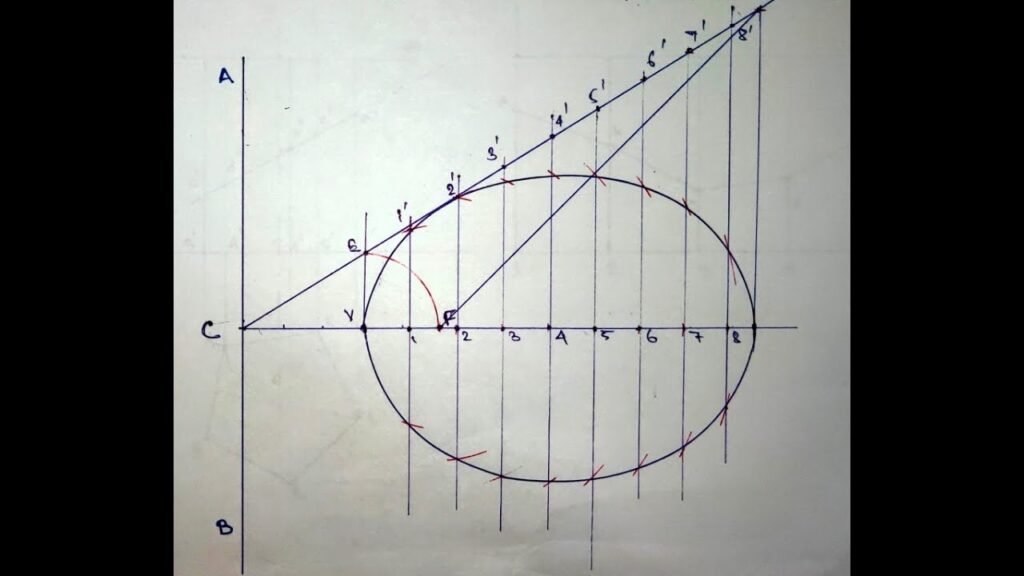
3. Name 2nd part from F as V (Vertex Point). It is 20 mm and 30 mm from F and AB line respectively. It is first point giving ratio of its distances from F and AB 2/3 i.e. 20/30.
4. For more points giving same ratio by tracing distance from first vertex points on vertex line towards right side in 8 or 12 equal parts.
5. Now draw vertical lines from vertex points up to approx length.
6. Now with first vertex point as centre and radius equal to F draw an arc which should intersect vertical line of first vertex point at upper side.
7. Join arc’s intersection point (with vertical line) with directrix point from which both (directrix and vertex) separates.
8. Give the numbers to the joined line at which it intersects with other vertical line from different vertex points.
9. Now take F as center and radius equal to 1a draw an arc on both sides of vertical line passing through 1 on both sides (upper and lower). Repeat the process for all vertex points by keeping center F as center.
10. Join all arcs as per their numbers which shows required curve ellipse by Directrix-Focus Method.