Fuzzy systems have been demonstrated their ability to solve different kinds of problems in classification, modeling control and in a considerable number of industry applications. It has been  shown  as  a  powerful  methodology  for  dealing  with  imprecision  and  nonlinearity efficiently  (Wang,  1994).  However,  one  of  the  shortcomings  of  fuzzy  logic  is  the  lack  of learning  and  adaptation  capabilities.  As  we  know,  neural  network  (NN)  is  one  of  the important technologies towards realizing artificial intelligence and machine learning. Many types  of  neural  networks  with  different  learning  algorithms  have  been  designed  and developed  (Deng  et  al.,  2002;  Levin  &  Narendra,  1996;  Narendra  &Parathasarathy,  1998). Recently, there is an increasing interest to hybridize the approximate reasoning method of fuzzy   systems   with   the   learning   capabilities   of   neural  networks   and   evolutionary algorithms.  Fuzzy neural  network (FNN) system is  one of the most successful and  visible directions of that effort.FNNs as hybrid systems have been proven to be able to reap the benefits of fuzzy logic and neural  networks.  In  these  hybrid  systems,  standard  neural  networks  are  designed  to approximate a fuzzy inference system through the structure of neural networks  while the parameters of the fuzzy system are modified by means of learning algorithms used in neural networks.  One  purpose  of  developing  hybrid  fuzzy  neural  networks  is  to  create  self- adaptive  fuzzy  rules  for  online  identification  of  a  singleton  or  Takagi-Sugeno-kang  (TSK) type fuzzy model (Takagi & Sugeno, 1985) of a nonlinear time-varying complex system. The twin  issues  associated  with  a  fuzzy  system  are  1)  parameter  estimation  which  involves determining parameters of premises and consequences and 2) structure identification which involves  partitioning  the  input space  and  determining  the  number  of  fuzzy  rules  for  a specific performance.  FNN systems have been found to be very effective and of widespread use in several fields.In  recent  years,  the  idea  of  self-organization  has  been  introduced  in hybrid  systems  to

create  adaptive  models.  Some  adaptive  approaches  also  have  been  introduced  in  FNNs whereby not only the weights but also the structure can be self-adaptive during the learning process ( Er & Wu, 2002; Huang et al., 2004; Jang, 1993; Juang &Lin, 1998; Leng et al., 2004; Lin &Lee, 1996; Qiao & Wang, 2008).

The technology of FNNs combines the profound learning capability of neural networks with the  mechanism  of  explicit  and  easily  interpretable  knowledge  presentation  provided  by fuzzy  logic.  In  a  word,  FNN  is  able  to  represent  meaningful  real-world  concepts  incomprehensive knowledge  bases.  The  typical  approach  of  designing  an  FNN  system  is  to build  standard  neural  networks  first,  and  then incorporate  fuzzy  logic  in  the  structure  of neural  networks.  The  key  idea  is  as  follows:  Assuming  that  some  particular  membership functions have been defined, we begin with a fixed number of rules by resorting to either trial-and-error methods or expert knowledge. Next, the parameters are modified by learning algorithm  such  as  backpropagation  (BP)  algorithm  (Siddique  &  Tokhi,  2001).  The  BP  is  a gradient  descent  search  algorithm.  It  is  based  on  minimization  of  the  total  mean  squared error  between  the  actual  output  and  the  desired  output.  This  error  is  used  to  guide  the search of the BP algorithm in the weight space. The BP is widely used in many applications in  that  it  is  not  necessary  to  determine  the  exact  structure  and  parameters  of  neural networks in advance. However, the problem of the BP algorithm is that it is often trapped in local minima and the learning speed is very slow in searching for global minimum of the search  space.  The  speed  and  robustness  of  the  BP  algorithm  are  sensitive  to  several parameters  of  the  algorithm  and  the  best  parameters  vary  from  problems  to  problems. Therefore,   many   adjustment   methods   have   been   developed,   notably   evolutionary algorithms  such  as  genetic  algorithms  (GAs)  or  particle  swarm  optimization  (PSO).  By working  with  a  population  of  solutions,  the  GA  can  seek  many  local  minima,  and  thus increase the likelihood of finding global minimum. This advantage of GA can be applied to neural  networks  to  optimize the  topology  and  parameters  of  weights.  The  key  point  is  to employ an evolutionary learning process to automate the designing of the knowledge base, which can be considered as an optimization or search problem. The GA is used to optimize the parameters  of neural networks (Seng et  al., 1999; Siddique & Tokhi, 2001; Zhou & Er,

2008)  or  identify  the  optimal  structure  of  neural  networks  (Chen  et  al.,  1999;  Tang  et al.,1995,). 

Moreover,  the  adaptation  of  neural  network  parameters  can  be  performed  by different methods such as orthogonal least square (OLS) (Chen et al.,1991), recursive least square (RLS) (Leng et al., 2004), linear least square (LLS) (Er & Wu, 2002), extended Kalman filter (EKF)  (Kadirkamanathan & Niranjan, 1993; Er et al., 2010) and so on.The objective of this chapter is to develop FNNs by hybrid learning techniques so that these systems can be used for online identification, model and control nonlinear and time-varying complex systems. In this chapter, we propose two kinds of self-organizing FNN that attempt to  combine fuzzy  logic  with  neural  network  and  apply  these  learning algorithms  to solve several  well-known  benchmark  problems  such  as  static  function  and  linear  and  nonlinear function  approximation,  Mackey-Glass  time-series  prediction  and  real-world  benchmark regression prediction and so on.The chapter is organized as follows. The general frame of self-organizing FNN is described in Section 2. The first learning algorithm combined FNN with EKF is presented in Section 3. It  is  simple  and  effective  and  is  able  to  generate  a  FNN  with  high  accuracy  and  compact structure. Furthermore, a novel neuron pruning algorithm based on optimal brain surgeon (OBS)  for  self-organizing  FNN  is  described  in  Section  4  in  detail.  Simulation  studies  on several well-known benchmark problems and comparisons with other learning algorithms have been conducted in each section. The summary of FNN associated with conclusions and future work are discussed in Section 5.

General frame of self-organizing FNNs

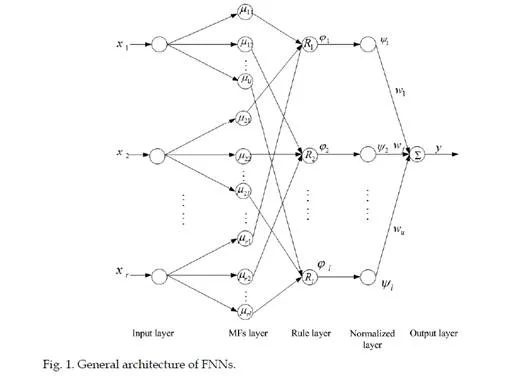
The  self-organizing  fuzzy  neural  network  system  primarily  implements  TSK  or  TS  type  (Sugeno & Kang, 1988) fuzzy model. The general architecture is depicted in Fig. 1. This five-layer self-organizing FNN implements a TSK type fuzzy system. Without loss of generality, we    consider    a    multi-input-single-output    (MISO)    fuzzy    model    with    input    vector X=(x₁,x₂,…,x_r) and output variable y.

Conclusions

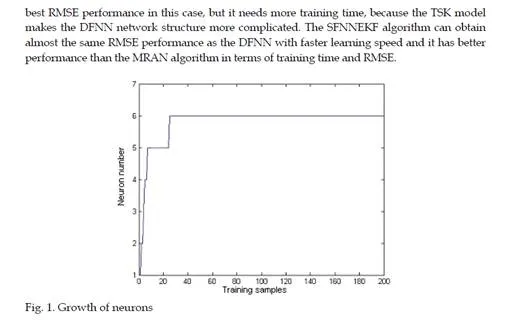
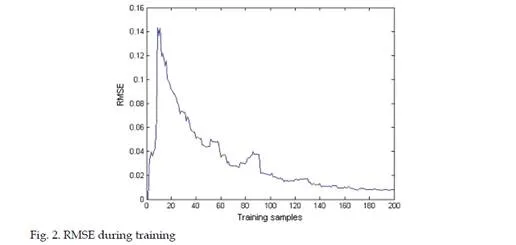
A new self-constructing fuzzy neural network has been proposed in this part. The basic idea of the proposed approach is to construct a self-constructing fuzzy neural network based on criteria of generating and pruning neurons. The EKF algorithm has been used to adapt the consequent parameters when a hidden unit is not added. The superior performance of the SFNNEKF over some other learning algorithms has been demonstrated in three examples in this  part.  Simulation  results  show  that  a  more  effective  fuzzy  neural  network  with  high accuracy   and   compact   structure   can   be   self-constructed   by   the   proposed   SFNNEKF algorithm.

An euronpruning algorithm based on optimal brain surgeon for self-organizing fuzzy neural networks with parsimonious structure

In this section, a novel learning algorithm for creating a self-organizing FNN to implement TSK  type  fuzzy  models  is  proposed.  The  optimal  brain  surgeon  (OBS)  (Hassibi  &  Stork, 1993) is employed as a neuron pruning mechanism to remove unimportant neurons directly during  the  training  procedure.  Distinguished  from  other  pruning  strategies  based  on  the OBS, there is no need to calculate the inverse matrix of Hessian, we simplify the calculation by  using  LLS  method  to  obtain  the  Hessian  matrix.  To  acquire  precision  model,  the  LLS method is  performed  to  obtain  the  consequent  parameters  of  the  network.  The  proposed algorithm   has   a   parsimonious   structure   and   is   generated   with   high   accuracy.   The effectiveness of the proposed algorithm is demonstrated in several well-known benchmark problems    such    as    static    function    approximation,    two-input    nonlinear    function approximation  and  real-world  non-uniform  benchmark  regression  problems.  Simulation studies are compared with other existing published algorithms. The results indicate that the proposed    algorithm    can    provide    comparable    approximation    and    generalization performance with a more compact structure and higher accuracy.

Learning algorithm of the FNN

The learning procedure of the proposed self-organizing FNN comprises two stages. In the first  stage,  the  structure  of  the  FNN  is  generated  based  on  the  growth  criteria  and  the proposed  OBS-based  pruning  method.  In  the  second  stage,  parameters  of  newly  created neurons are assigned and consequent parameters of all existing neurons will be updated by the LLS method.

StructuredesignoftheFNN

To determine the proper number of neurons or fuzzy rules of FNNs, we adopt two growth criteria to generate neurons. In order to obtain a compact structure, the OBS algorithm (Hassibi&  Stork,  1993)  is  employed  as  a  pruning  criterion.  An  initial  structure  of  the  FNN  is  first constructed and the importance of each hidden neuron or fuzzy rule is evaluated by the OBS algorithm, the least important neuron will be deleted if the performance of the entire network is accepted after deleting this unimportant neuron. This procedure will repeat until the desired accuracy can be satisfied. We will describe the learning algorithm in detail in the sequel.The learning stage is based on a data set composed by n input-output pairs:

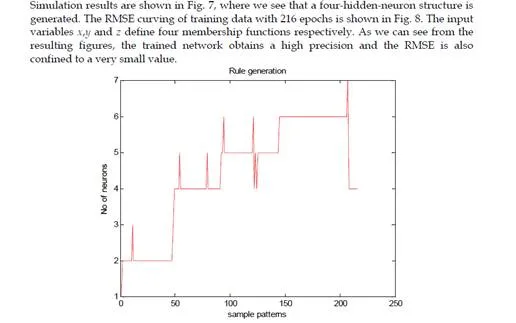
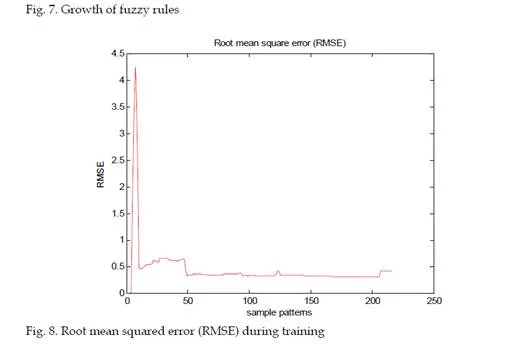
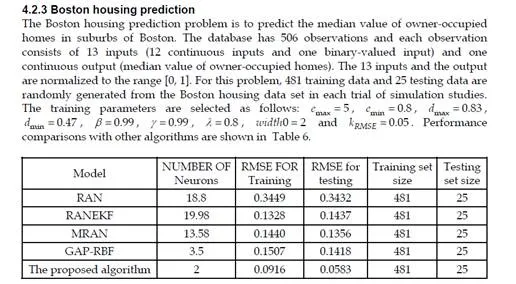
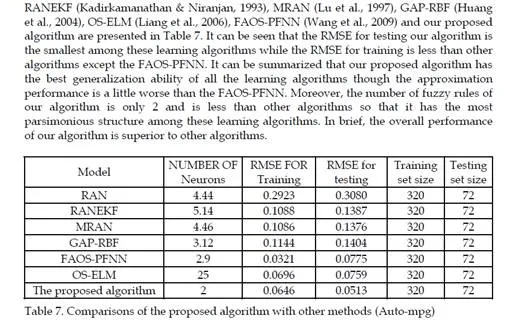
Discussions

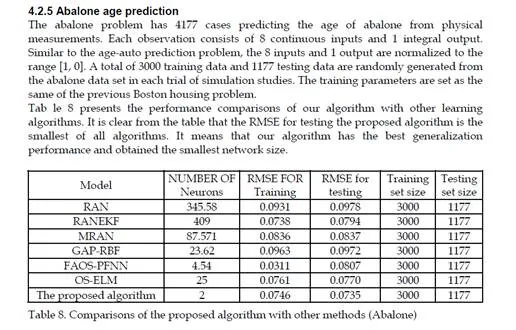
In this part a novel learning algorithm for creating a self-organizing fuzzy neural network (FNN)   to  implement   the   TSK  type   fuzzy  model   with  a   parsimonious   structure   was proposed.  The  OBS  is  employed  as  a  pruning  algorithm  to  remove  unimportant  neurons directly during the training process. Apart from other pruning strategies based on the OBS, there is no need to calculate the inverse matrix of Hessian; we simplify the calculation by using the LLS method to obtain the Hessian matrix.The  effectiveness  of  the  proposed  algorithm  has  been  demonstrated  in  four  well-known benchmark  problems:  namely  static  function  approximation,  nonlinear  dynamic  system identification,   two-input   nonlinear   function   and   real-world   non-uniform   benchmark problems.  Moreover,  performance  comparisons  with  other  learning  algorithms  have  also been  presented  in  this  part.  The  results  indicate  that  the  proposed  algorithm  can  provide comparable   approximation  and   generalization   performance   with   a   more   compact parsimonious structure and higher accuracy.

Conclusions and future work

In  this  chapter,  the  development  of  fuzzy  neural  networks  has  been  reviewed  and  the main issues for designing fuzzy neural networks including growing and pruning criteria and  different  adjustment  methods  of  consequent  parameters  have  been  discussed.  The general  frame  of  fuzzy  neural  networks  based  on  radial  basis  function  neural  networks has  been  described  in  Section  2.  Two  self-organization  FNNs  have  been  developed.  For the   first   FNN,   the  SFNNEKF   algorithm  employs  ERR   as  a   generation  condition   in constructing the network which makes the growth of neurons smooth and fast. The EKF algorithm  has  been  used  to  adjust  free  parameters  of  the  FNN  to  achieve  an  optimal solution.  Simulation  results  show  that  a  more  effective  fuzzy  neural  network  with  high accuracy  and  compact  structure  can be  self-constructed  by  the  proposed  SFNNEKF algorithm. For the second FNN, it is composed of two stages: the structure identification stage   and   the   parameter   adjustment   stage.   The   structure   identification   consists   of constructive and pruning procedures. An initial structure starts with no hidden neurons or fuzzy rule sets and grows neurons based on the criteria of neuron generation. Then the OBS is employed as a pruning strategy to further optimal the obtained initial structure. At last, the well-known LLS method is adopted to tune the free parameters in the parameter adjustment  stage  for  sequentially  arriving  training  data  pairs.  Simulation  studies  are compared  with  other  algorithms.  The  simulation  results  indicate  that  the  proposed algorithm can provide comparable approximation and generalization performance with a more compact structure and higher accuracy.

In a word, fuzzy neural networks are hybrid systems that combine the advantages of fuzzy logic  and  neural  networks,  there  existed  many  kinds  of  FNN  developed  by  researchers. Recently, the idea of self-organizing has been introduced in FNN. The purpose is to develop self-organizing fuzzy neural network systems to approximate fuzzy inference through the structure of neural networks to create adaptive models, mainly for approximate linear and nonlinear and time-varying systems. FNNs have been widely used in many fields. For our future work, studies will focus on the structure learning since appropriate number of fuzzy rules  or  find  proper  network  architecture  and  developing  optimal  parameter  adjustment methods.