Face  Recognition  by  a  robot  or  machine  is  one  of  the  challenging  research  topics  in  the recent years. It has become an active research area which crosscuts several disciplines such as  image  processing,  pattern  recognition,  computer  vision,  neural  networks  and  robotics. For   many   applications,   the   performances   of   face   recognition   systems   in   controlled environments have achieved a satisfactory level. However, there are still some challenging issues  to  address  in  face  recognition  under  uncontrolled  conditions.  The  variation  in illumination is one of the main challenging problems that a practical face recognition system needs  to  deal  with.  It  has  been  proven  that  in  face  recognition,  differences  caused  by illumination variations are more significant than differences between individuals (Adini et al., 1997). Various methods have been proposed to solve the problem. These methods can be classified   into   three   categories,   named   face   and   illumination   modeling,   illumination invariant  feature  extraction  and  preprocessing  and  normalization.  In  this  chapter,  an extensive and state-of-the-art study of existing approaches to handle illumination variations is presented. Several latest and representative approaches of each category are presented in detail,   as   well   as   the   comparisons   between   them.   Moreover,   to   deal   with   complex environment where illumination variations are coupled with other problems such as pose and expression variations, a good feature representation of human face should not only be illumination invariant, but also robust enough against pose and expression variations. Local binary pattern (LBP) is such a local texture descriptor. In this chapter, a detailed study of the LBP and its several important extensions is carried out, as well as its various combinations with  other  techniques  to  handle  illumination  invariant  face  recognition  under  a  complex environment.  By  generalizing  different  strategies  in  handling  illumination  variations  and evaluating  their  performances,  several  promising  directions  for  future  research  have  been suggested.This  chapter  is  organized  as  follows.  Several  famous  methods  of  face  and  illumination modeling are introduced in Section 2. In Section 3, latest and representative approaches of illumination invariant feature extraction are presented in detail. More attentions are paid on quotient-image-based methods. In Section 4, the normalization methods on discarding low frequency  coefficients  in  various  transformed  domains  are  introduced  with  details.  In Section  5,  a  detailed  introduction  of  the  LBP  and  its  several  important  extensions  is presented,  as  well  as  its  various  combinations  with  other  face  recognition  techniques.  In Section 6, comparisons between different methods and discussion of their advantages and disadvantages  are  presented.   Finally,  several  promising  directions  as  the  conclusions  are drawn in Section 7.

Face and illumination modelling

Here, two kinds of modeling methods named face modeling and illumination modeling will be introduced. Regarding face modeling, because illumination variations are mainly caused by  three-dimension  structures  of  human  faces,  researchers  have  attempted  to  construct  a general 3D human face model in order to fit different illumination and pose conditions. One straight way is to use specific sensors to obtain 3D images representing 3D shape of human face.  A  range  image,  a  shaded  model  and  a  wire-frame  mesh  are  common  alternatives representations  of  3D  face  data.  Several  detailed  surveys  on  this  area  can be  referred  to Bowyer et al. (2006) and Chang et al. (2005). Another way is to map a 2D image onto a 3D model and the 3D model with texture is used to produce a set of synthetic 2D images, with the  purpose  of  calculating  the  similarity  of  two  2D  images  on  the  3D  model.  The  most representative method is the 3D morphable model proposed by Blanz & Vetter (2003) which describes  the  shape  and  texture  of  a  human  face  under  the  variations  such  as  poses  and illuminations.  The  model  is  learned  from  a  set  of  textured  3D  scans  of  heads  and  all parameters are estimated by maximum a posteriori estimator. In this framework, faces are represented by model parameters of 3D shape and texture. High computational load is one of the disadvantages for this kind of methods.

For illumination variation modeling, researchers have attempted to construct images under different  illumination  conditions.  Modeling  of  face  images  can  be  based  on  a  statistical model or a physical model. For statistical modeling, no assumptions concerning the surface is  needed.  The  principal  component  analysis  (PCA)  (Turk  &  Pentland,  1991)  and  linear discriminant  analysis  (LDA)  (Etemad  &  Chellappa,  1997;  Belhumeur  et  al.,  1997) can  be classified  to  the  statistical  modeling.  In  physical  modeling,  the  model  is  based  on  the assumption of certain surface reflectance properties, such as Lambertian surface (Zou et al.,

2007). The famous Illumination Cone, 9D linear subspace and nine point lights all belong to the illumination variation modeling.

In (Belhumeur & Kriegman 1998), an illumination model illumination cone is proposed for the first time. The authors proved that the set of n-pixel images of a convex object with a Lambertian reflectance function, under an arbitrary number of point light sources at infinity, formed  a  convex  polyhedral  cone  in  IRⁿ    named  as  illumination  cone  (Belhumeur  & Kriegman 1998). If there are k point light sources at infinity, the image X of the illuminated object can be modeled as

reflectance  function,  seen  under  all  possible  illumination  conditions,  still  forms  a  convex cone in IRⁿ. The paper also extends these results to colour images. Based on the illumination cone model, Georghiades et al. (2001) presented a generative appearance-based method for recognizing human faces under variations in lighting and viewpoint. Their method exploits the illumination cone model and uses a small number of training images of each face taken with different lighting directions to reconstruct the shape and albedo of the face. As a result, this  reconstruction  can  be  used  to  render  images  of  the  face  under  novel  poses  and illumination   conditions.   The   pose   space   is   then   sampled,   and   for   each   pose   the corresponding  illumination  cone  is  approximated  by  a  low-dimensional  linear  subspace whose basis vectors are estimated using the generative model. Basri  and  Jacobs  (2003)  showed  that  a  simple  9D  linear  subspace  could  capture  the  set  of images of Lambertian objects under distant, isotropic lighting. Moreover, they proved that the

9D linear space could be directly computed from a model, as low-degree polynomial functions of its scaled surface normals. Spherical harmonics is used to represent lighting and the effects of Lambertian materials are considered as the analog of a convolution. The results help them to construct algorithms for object recognition based on linear methods as well as algorithms that use convex optimization to enforce non-negative lighting functions. Lee  et  al.  (2005)  showed  that  linear  superpositions  of  images  acquired  under  a  few directional  sources  are  likely  to  be  sufficient  and  effective  for  modeling  the  effect  of illumination on human face. More specifically, the subspace obtained by taking k images of an object under several point light source directions with k typically ranging from 5 to 9, is an  effective  representation  for  recognition  under  a  wide  range  of  lighting  conditions. Because  the subspace  is  constructed  directly from  real  images,  the  proposed  methods  has the following advantages, 1)potentially complex steps can be avoided such as 3D model of surface  reconstruction;  2)  large  numbers  of  training  images  are  not  required  to  physically construct complex light conditions.

In  addition  to  the  assumption  that  the  human  face  is  Lambertian  object,  another  main drawback  of  these  illumination  modeling  methods  is  that  several  images  are  required  for modeling.

Illumination in variant feature extraction

The  purpose  of  these  approaches  is  to  extract  facial  features  that  are  robust  against illumination  variations.  The  common  representations  include  edge  map,  image  intensity derivatives  and  Gabor-like  filtering  image  (Adini  et  al.,  1997).  However,  the  recognition experiment   on   a   face   database   with   lighting   variation   indicated   that   none   of   these representations was sufficient by itself to overcome the image variation due to the change of illumination direction (Zou et al., 2007).Recently, quotient-image-based methods are reported to be a simple and efficient solution to illumination variances and have become one active research direction. Quotient Image (QI) (Amnon  &  Tammy,  2001)  is  defined  as  image  ratio  between  a  test  image  and  linear combinations  of  three  unknown  independent  illumination  images.  The  quotient  image depends  only  on  the  relative  surface  texture  information  and  is  free  of  illumination. However, the performance of QI depends on the bootstrap database. Without the bootstrap database and known lighting conditions, Wang et al. (2004a; 2004b) proposed Self-Quotient Image (SQI) to solve the illumination variation problem. The salient feature of the method is to estimate luminance using the image smoothed up by a weighted Gaussian filter. The SQI is defined as

the  center  point  in  the  convolution  region  is  larger  than  an  empirical  threshold,  and each image  is  convolved  twice.  For  the   normalization  on  large-scale  image,  two  different methods, the DCT (Chen et al., 2006) and the non-point light quotient image (NPL-QI), are separately applied to large-scale image. The experimental results on the CMU PIE and Yale B as well as the Extended Yale B database show that the proposed framework outperforms existing methods. In  addition  to  the  quotient-image-based  methods,  local  binary  pattern  (LBP)  is  another attractive  representation  of  facial  features.  Local  descriptors  of  human  faces  have  gained attentions  due  to  their  robustness  against  the  variations  of  pose  and  expression.  The  LBP operator is one of the best local texture descriptors. Besides the robustness against pose and expression variations as common texture features, the LBP is also robust to monotonic gray- level  variations  caused  by  illumination  variations.  The  details  of  the  LBP  and  several important extensions of the operator will be introduced in the following section, as well as its   various   combinations   with   other   techniques   to   handle   illumination   invariant   face recognition under a complex environment.

Pre-processing and normalization

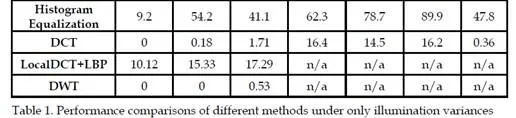
In this kind of approaches, face images under illumination variations are preprocessed so that images under normal lighting can be obtained. Further recognition will be performed based on the normalized images. Histogram Equalization (Gonzales & Woods, 1992) is the most commonly used method. By performing histogram equalization, the histogram of pixel intensities in the resulting images is flat. Therefore improved performances can be achieved after  histogram  equalization.  Adaptive  histogram  equalization  (Pizer  &  Amburn,  1987), region-based   histogram   equalization   (Shan   et   al.,   2003),   and   block-based   histogram equalization  (Xie  &  Lam,  2005)  are  several  important  variants  of  the  HE  and  obtain  good performances. Recently,  the  methods  on  discarding  low  frequency  coefficients  in  various  transformed domains are reported to be simple and efficient solutions to tackle illumination variations and have become one active research direction. In (Chen et al., 2006), the image gray value level  f(x,y)  is  assumed  to  be  proportional  to  the  product  of  the  reflectance  r(x,y)  and  the illumination e(x,y) i.e.,

Based  on  Chen’s  idea,  Vishwakarma  et  al.  (2007)  proposed  to  rescale  low-frequency  DCT coefficients to lower values instead of zeroing them in Chen’s. In (Vishwakarma et al., 2007), the  first  20  low  frequency  DCT  coefficients  are  divided  by  a  constant  50,  and  the  AC component is then increased by 10%. Although they presented some comparisons of figures to  demonstrate the  effect  of the  proposed method  compared  to  the original  DCT  method, there is no experimental result to prove the effect of the proposed method for recognition task.  Besides,  it  is  difficult  to  choose  the  value  of  rescale  parameter  only  by  experiences. Perez and Castillo (2008) also proposed a similar method which applied Genetic Algorithms to  search  appropriate  weights  to  rescale  low-frequency  DCT  coefficients.  Two  different strategies of selecting the weights are compared. One is to choose a weight for each DCT coefficient and the other is to divide the DCT coefficients into small squares, and choose a weight  for  each  square.  The  latter  strategy  reduces  the  computational  cost  because  fewer weights are required to choose. However, the GA still takes a large computational burden and the obtained weights depend on the training figures. As mentioned in the last section, the local binary patterns (LBP) operator is one of the best local texture descriptors. Because of its robustness against pose and expression variations as well  as  monotonic  gray-level  variations  caused  by  illumination  variations,  Heydi  et  al. (2008)  presented  a  new  combination  way  of  using  the  DCT  and  LBP  for  illumination normalization. Images are divided into blocks and the DCT is applied in each block. After that, the LBP is used to represent facial features because the LBP can represent well facial structures  when  variations  in  lights  are  monotonic.  The  experimental  results  demonstrate the  proposed  method  can  achieve  good  performances  when  several  training  samples  per person are used. However, in the case where only one frontal image per person is used for training,  which  is  common  in  some  practical  applications,  the  performance  cannot  be satisfactory especially in the cases with larger illumination variations.

Besides  the  DCT,  discrete  wavelet  transform  (DWT)  is  another  common  method  in  face recognition.  There  are  several  similarities  between  the  DCT  and  the  DWT:  1)  They  both transform the data into frequency domain; 2) As data dimension reduction methods, they are both independent of training data compared to the PCA. Because of these similarities, there  are  also  several  studies  on  illumination  invariant  recognition  based  on  the  DWT. Similar to the idea in (Chen et al., 2006), a method on discarding low frequency coefficients of the DWT instead of the DCT was proposed (Nie et al., 2008). Face images are transformed from spatial domain to logarithm domain and 2-dimension wavelet transform is calculated by   the   algorithm.   Then   coefficients   of   low-low   subband   image   in   n-th   wavelet decomposition are discarded for face illumination compensation in logarithm domain. The experimental results prove that the proposed method outperforms the DCT and the quotient images. The kind of wavelet function and how many levels of the DWT need to carry out are the key factors for the performance of the proposed method. Different from the method in (Nie et al., 2008), Han et al. (2008) proposed that the coefficients in low-high, high-low and high-high  subband  images  were  also  contributed  to  the  effect  of  illumination  variation besides the low-low subband images in n-th level. Based on the assumption, a homomorphic filtering is applied to separate the illumination component from the low-high, high-low, and high-high subband images in all scale levels. A high-pass Butterworth filter is used as the homomorphic  filter.  The  proposed  method  obtained  promising  results  on  the  Yale  B  and CMU PIE databases.

where  F’(m,n)  is  the  gray  level  of  the  point  under  the  illumination  G(m,n),  F(m,n)  is  the original face image, and B(m,n)  is the background noise which is assumed to change slowly. In (Gu et al., 2008), the background noise is estimated and eliminated by multi-level wavelet decomposition  followed  by  spline 

Illumination in variant face recognition under complex environment

interpolation.  After  that,  the  effect of  illumination  is removed   by  the   similar   multi-level   wavelet   decomposition   in   the  logarithm   domain. Experimental  results  on  Yale  B  face  database  show  that  the  proposed  method  achieves superior  performance  compared  to  the  others.  However,  by  comparing  the  results  of  the proposed method and the DCT, we find the result of the proposed method is worse than that of the DCT. Hence, the proposed method is not as effective as the DCT for illumination invariant recognition. The novelty of the proposed method is that the light variation in an image  can  be  modeled  as  multiplicative  noise  and  additive  noise,  instead  of  only  the multiplicative   term   in   (11),   which   may   be   instructive   in   modeling  the   face   under illumination variations in future.

In  fact,  there  is  seldom  the  case  in  practical  applications  that  only  illumination  variations exist.  Illumination  variations  are  always  coupled  with  pose  and  expression  variations  in practical   environments.   To   deal   with   such   complex   environment,   an   ideal   feature representation  of  human  face  should  not  only  be  illumination  invariant,  but  also  robust enough  against  pose  and  expression  variations.  Local  descriptors  of  human  faces  have gained attentions due to their robustness against the variations of pose and expression. The local binary patterns (LBP) operator is one of the best local texture descriptors. The operator has  been  successfully  applied  to  face  detection,  face  recognition  and  facial  expression analysis.  In  this  section,  we  will  present  a  detailed  introduction  of  the  LBP  and  several important  extensions  of  the  operator,  as  well  as  its  various  combinations  with  other techniques to handle illumination invariant face recognition under a complex environment. The original LBP operator was proposed for texture analysis by Ojala et al. (1996). The main idea in LBP is to compare the gray value of central point with the gray values of other points in the neighborhood, and set a binary value to each point based on the comparison. After that, a binary string is transformed to a decimal label as shown in the following equation

on a pixel- level, the labels are summed over a small region to produce information on a regional level and an entire histogram concatenated by regional histograms presents a global description of the image (Ahonen et al., 2004). Because of the features, the LBP operator is considered as one of the best local texture descriptors. Besides the robustness against pose and expression variations  as  common  texture  features,  the  LBP  is  also  robust  to  monotonic  gray-level variations caused by illumination variations. It is evident that different regions on the face have different discriminative capacities. Therefore, different regions are assigned different weights in similarity measurement. In (Hadid et al., 2004), with the purpose of dealing with face  detection  and  recognition  in  low-resolution  images,  the  LBP  operator  was  applied  in two-level hierarchies, regions and the whole image. In the first level, LBP histograms were extracted from the whole image as a coarse feature representation. Then, a finer histogram, extracted  from  smaller  but  overlapped  regions,  was  used  to  carry  out  face  detection  and recognition further. In (Jin et al., 2004), the author pointed out that the original LBP missed the local structure under some certain circumstance because the central point was only taken as a threshold. In order to obtain all the patterns in a small patch such as 3*3, the mean value of the patch was taken as a threshold instead of the gray level of the central point. Because the central point provides more information in most cases, a largest weight is set to it as following equation

Because of the extension, the LTP is more discriminant and less sensitive to noise. To apply the  uniform  pattern  in  the  LTP,  a  coding  scheme  that  split  each  ternary  pattern  into  its positive and negative halves is also proposed in (Tan & Triggs, 2010). The resulted halves can be treated as two separated LBPs and used for further recognition task. From another point of view, the LBP can be considered as the descriptor of the first derivation information  in  local  patch  of  the  image.  However  they  only  reflect  the  orientation  of  local variation and could not present the velocity of local variation. In order to solve the problem, Huang  et  al.  (2004)  proposed  to  apply  the  LBP  to  Sobel  gradient-filtered  image  instead  of original image. Jabid et al. (2010) proposed local directional pattern which was obtained by computing the edge response value in all eight direction at each pixel position and generating a  code  from  the  relative  strength  magnitude.  The  local  directional  pattern  is  more  robust against noise and non-monotonic illumination changes. Moreover, a high-order local pattern descriptor,  local  derivative  pattern  (LDP),  was  proposed  by  Zhang  et  al.  (2010).  LDP  is  a general framework which describes high-order local derivative direction variations instead of only the first derivation information in the LBP. Based on the experimental results, the third- order LDP can capture more detailed discriminative information than the second-order LDP and the LBP. The details of the LDP can be referred to (Zhang et al., 2010). The experimental results in (Ahonen et l.,2006) proved that the LBP outperformed other texture  descriptors  and  several  existing  methods  for  face  recognition  under  illumination variations. However, the LBP is still not robust enough against larger illumination variations in practical applications. Several other techniques are proposed to combine with the LBP to tackle face recognition under complex variations. In addition to the DCT as mentioned in the last section, Gabor wavelets are also promising candidates for combination.

The LBP is good at coding fine details of facial appearance and texture, while Gabor features provide a coarse  representation  of  face  shape  and  appearance.  In  (Zhang  et  al.,  2005),  a  local  Gabor binary  pattern  histogram  sequence  (LGBPHS)  method  was  proposed  in  which  Gabor wavelet filters were used as a preprocessing stage for LBP feature extraction. The LBP was applied in different Gabor wavelets filtered image instead of the original images and only Gabor  magnitude  pictures  were  used  because  Gabor  phase  information  were  considered sensitive to position variations. To overcome the problem, Xie et al. (2010) proposed a novel framework to fuse LBP features of Gabor magnitude and phase images. A local Gabor XOR patterns (LGXP) was developed whose basic idea was that two phases were considered to reflect similar local features if two phases belonged to the same interval. Furthermore, the paper  presented  two  methods  to  combine  local  patterns  of  Gabor  magnitude  and  phase, feature-level  and  score-level.  In  the  feature-level,  two  different  local  pattern  histograms were  simply  concatenated  into  one  histogram  and  the  resulting  histogram  was  used  for measuring  similarity.  In  the  score-level,  two  different  kinds  of  histograms  were  used  to compute similarities respectively and then two similarity scores were fused together based on a weighted sum rule.

Comparisons and discussions

In  this  section,  we  will  compare  different  methods  and  discuss  their  advantages  and disadvantages.  To  evaluate  the  performances  of  different  methods  under  varying  lighting conditions without other variances, there are three popular databases, the Yale B, Extended Yale  B  and  CMU  PIE  database.  In  the  Yale  Face  database  B,  there  are  64  different illumination  conditions  for  nine  poses  per person  (Georghiades  et  al.,  2001).  To  study the performances  of  methods  under  different  light  directions,  the  images  are  divided  into  5 subsets based on the angle between the lighting direction and the camera axis. The Extended Yale B database consists 16128 images of 28 subjects with the same condition as the Original Yale  B  (Lee  et  al.,  2005).  In  the  CMU  PIE,  there  are  altogether  68  subjects  with  pose, illumination and expression variations (Sim et al., 2003). Because we are concerned with the illumination  variation  problem,  only  21  frontal  face  images  per  person  under  different illumination conditions are chosen, totally 1421 images.

The performances of several representative approaches of each category are shown in Table1.  The  results  are  directly  referred  from  their  papers  since  they  are  based  on  the  same database. It can be seen that several methods achieved satisfactory performance. However, each  technique  still  has  its  own  drawbacks.  High  computational  load  is  one  of  the  main disadvantages for face modeling. For illumination modeling methods, most of them require several  training  images.  Besides,  as  mentioned  before,  physical  illumination  modeling generally is based on the assumption that the surface of the object is Lambertian, which is not consistent with the real human face. Regarding the illumination invariant features, most of them even the QI-based methods are still not robust enough against larger illumination variation.  The  LTV  and  TVQI  obtain  the  best  performances  among  all  the  mentioned methods.  However,  they  are  very  time  consuming  because  they  needs  to  find  an  optimal solution  to  decompose  face  images  step  by  step.  Compared  to  QI-based  methods,  the methods  on  discarding  low  frequency  coefficients  in  various  transformed  domains  are easier to implement and usually have lower computational costs because QI-based methods need  to  estimate  albedo  point  by  point.  The  performances  of  the  methods  discarding  low frequency coefficients are also good    but still not satisfactory as QI-based methods. In fact, illumination variations and facial features cannot be perfectly separated based on frequency components, because some facial features also lie in the low-frequency part as illumination variations. Therefore, some facial information will be lost when low-frequency coefficients are   discarded.   Furthermore,   the   performance   of   illumination   normalization   methods generally  depends  on  the  choices  of  parameters,  most  of  which  are  determined  only  by experience and cannot be suitable for different cases.

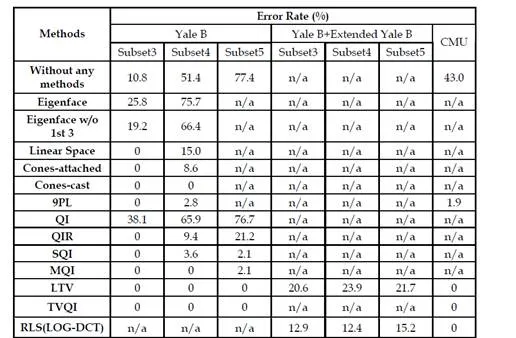
In addition to the above drawbacks of each category, there are some other issues. Firstly, the experiments of most of the methods are based on aligned images whose important points are  manually  marked.  The  sensitivity  of  the  methods  to  misalignment  is  seldom  studied except  some  SQI-based  methods.  Secondly,  the  common  experimental  databases  are  not very promising because of the small size and limited illumination variations. For instance, the Yale B database only contains 10 subjects and the CMU PIE database contains limited illumination   variations.   When   the   database   is   larger   and   contains   more   illumination variations,  the  outstanding  performances  of  existing  methods  may  not  be  sure.  The  LTV achieves  excellent  performance  in  (Chen  et  al.,  2006)  when  the  Yale  B  database  is  used. While  the  Extended  Yale  B  database  containing  more  subjects  (28)  is  used  as  the  test database in (Xie et al., 2008), the performance drops significantly as shown in Table 1.To evaluate the performances of methods under a complex environment where illumination variances coupled with other variances, FERET is the most popular database which contains

1196 subjects with expression, lighting and aging variations. In addition to the gallery set fa,there are four probe sets, fb ( 1195 images with expression variations), fc (194 images with illumination  variations), dup  I  (722  images with  aging  variations)  and dup  II  (234  images with larger aging variations). The performances of common methods, the LBP and several extensions  and  combinations  of  the  LBP  are  shown  in  Table  2.  The  results  are  directly referred from their papers since they are based on the same database

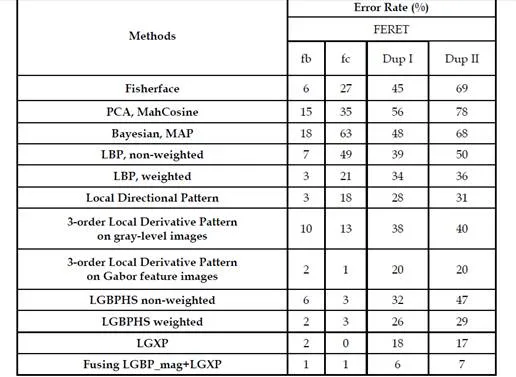
By  comparing  experimental  results  on  table 2,  we  can  easily  find  that  the  performance  of most LBP-based method can outperform other methods under expression, illumination and aging  variations.  However,  considering  the  performances  of  LBP-based  methods  in  the probe  set  fc  with  illumination  variation,  we  can  easily  find  that  quotient-image-based methods  outperform  most  of  LBP-based  methods.  But  it  still  can  be  an  effective  and promising research direction because of its robustness against other variations such as aging and  expression  variations.  There  is  seldom  the  case  in  practical  applications  that  only illumination   variations   exist.   Illumination   variations   are   always   coupled   with   other variations   in   practical   environments.   Furthermore,   after   the   combination   with   Gabor features such as the weighted LGBPHS, LGXP and fusing method of LGBP and LGXP, the performances  of  LBP-based  methods  obtain  significant  improvements  and  even  achieve comparable   level   with   quotient-image-based   methods   under   illumination   variations. Hence,  the  LBP  can  be  employed  to  carry  out  face  recognition  in  a  complex  practical environment, combined with other recognition techniques such as Gabor wavelets.

Conclusions

In  summary,  the  modeling  approach  is  the  fundamental  way  to  handle  illumination variations,  but  it  always  takes  heavy  computational  burden  and  high  requirement  for  the number  of  training  samples.  For  illumination  invariant  feature,  the  quotient-image-based method  is  a  promising  direction.  The  LBP  is  also  an  attractive  area  which  can  tackle illumination  variation  coupled  with  other  variations  such  as  pose  and  expression.  For normalization  methods,  the  methods  on  discarding  low-frequency  coefficients  are  simple but  effective  way  to  solve  the  illumination  variation  problem.  However,  a  more  accurate model needs to be studied instead of simply discarding low-frequency coefficients. In a real complex condition, the LBP combined with other techniques such as Gabor wavelets is an easier  and  more  promising  way  to  deal  with  illumination  variances  coupled  with  other variances.