Modern nanotechnology includes several promising areas such as nano-optics, nano-photonics, nanochemistry, nanobiology, and nanomedicine. During the past decade, we have witnessed a tremendous growth of nanoparticle applications that require particles of different materials with different size, dispersion, shape, and morphology. As a result, the development of new nanoparticle synthesis methods is particularly important. Among the rapidly immerged techniques, plasma-based synthesis has a number of advantages being both rather simple and allowing unique and well-controlled formation of nanoparticles.
In particular, plasmas created by both pulsed laser ablation and by spark discharges can be used for nanoparticle synthesis. That is why these two techniques have attracted particular attention and resulted in numerous experimental and theoretical investigations. On one hand, the main advantage of laser ablation method, as was demonstrated in these studies, is the possibility to preserve target stoichiometry. On the other hand, spark discharge allows one to produce a very large amount of nanoparticles by using parallel multidischarge set-up. However, the main physical mechanisms involved in these processes stay partly puzzling. That is why additional studies based on a detailed comparison of both methods are required for the determination of their main similarities and differences.
Starting from the early 1990s, laser ablation (LA) has been intensively studied first for long laser pulses and then for much shorter ones [1-2]. A number of experiments revealed that laser interactions with solid targets lead to the formation of nanoparticles. Furthermore, if femtosecond laser is used, an explosive ejection of a mixture of clusters and atoms was both theoretically predicted and experimentally observed [3]. It was found that the produced nanoparticles demonstrated either plasmonic or photoluminescent properties, as well as a capacity of field amplification. These properties are particularly interesting biomedical applications, such as imaging and photodynamic therapy. It should be noted that absence of incompatibility with biological tissues is crucial for further development of most of the applications where nanoparticles are used in vivo. However, toxicity is hard to avoid in traditional chemical methods. In addition, the stability of these nanoparticles is still not high enough. It was demonstrated, fortunately, that nanoparticles produced by laser ablation are better suitable for biomedical applications, in particular, when they are produced in liquids [4].
This advantage made LA a unique tool for nanoparticle synthesis.In order to elucidate the physical mechanisms of LA, many analytical and numerical investigations were performed [5 -11]. In vacuum, self-similar adiabatic models with condensation were proposed [10-11]. In the presence of a gas, only either very low or high background pressure was used in most of the models for simplicity. Shock waves were shown to be produced during the plume expansion in a high-pressured background gas [3]. In this case, a system of Navier-Stocks equations well describes the first 1–2 μs of the plasma plume expansion. It should be noted that such models are invalid at the later stages. To solve this issue, hydrodynamic calculations were switched to the direct Monte Carlo simulations where no such hypothesis is used at 1–2 µs after the laser pulse [11, 12]. Recently, such approaches as molecular dynamics (MD), hydrodynamics (HD), and combinations with the direct simulation Monte Carlo method (DSMC) were proposed for picosecond and femtosecond laser interactions [13-14]. The initial stage of laser ablation process can be examined by using either hydrodynamic models or atomistic simulation. On one hand, the main advantage of numerical hydrodynamics is in the calculation rapidity and in the possibility to reach rather larger scales [10, 13]. Atomistic simulations, on the other hand, are not based on equilibrium assumptions and can more easily provide size distributions of nanoparticles. In particular, two-temperature molecular dynamics simulations (TTM-MD) were performed for femtosecond laser ablation of metals [14, 15].
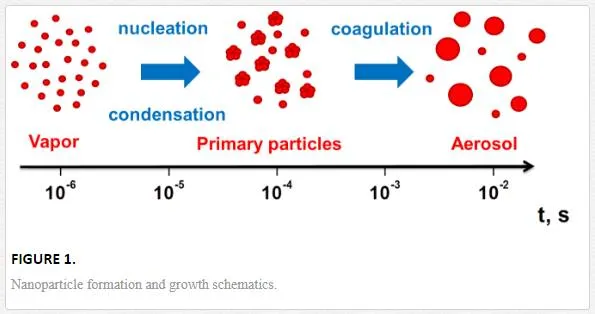
In the presence of a sufficiently high-pressured background environment, such as atmospheric pressured gas or a liquid, diffusion-driven nucleation and aggregation processes start playing an important role (Figure 1) at longer delays [16].
However, despite a growing interest in LA, some of its basic mechanisms remain not enough understood. The challenge is that ablation processes strongly depend on the ensemble of such parameters as temporal pulse width and shape, on laser wavelength, on the size of the laser spot, laser intensity, repetition rate, as well on the target material and background conditions. [17]
In spark discharges (SD), a typical set-up consists of two electrodes connected to a charged capacitance [16]. When high enough voltage V0 is applied, a so-called streamer is formed first. Once it reaches the opposite electrode, plasma breakdown takes place, followed by the streamer transition to an expanding plasma column. In this column, Joule heating of both plasma and electrodes take place. In addition, electrodes are bombarded by energetic ions that induce sputtering, which can be considered to be similar to laser ablation. If background gas is present, rapid thermalization of the sputtered material leads to primary nanoparticle formation that can then grow by collisions and form larger particles or aggregates.
Numerical modeling of spark discharge consists of several steps with rather different time scales [16]:
(i) streamer formation and propagation between electrodes;
(ii) streamer-to-spark transition;
(iii) gas heating and cylindrical expansion,
(iv) electrode evaporation and erosion;
(v) nanoparticles formation. Nanoparticle formation, here as in the case of laser ablation in the presence of a gas or a liquid, includes nucleation and collisional growth (Figure 1).
This work is aimed at the better understanding of the mechanisms involved in nanoparticle formation by laser ablation and by spark discharge. First, laser ablation is considered by using both atomistic and hydrodynamic numerical methods. In particular, mechanisms of nanoparticle formation and the corresponding conditions are analyzed. Then, attention is focused on the role of the background environment and its role in nanoparticle formation. These results are used to explain several recent experimental results.Second, spark discharge is investigated. Plasma properties and conditions required for nanoparticle formation are examined. Finally, we compare laser ablation and spark discharge as promising methods of nanoparticle formation.
Laser ablation
To examine ultra-short, laser-ablated plume dynamics and nanoparticle evolution under realistic experimental conditions and to account for the fact that the ablated plume contains several components, DSMC calculations of the plume dynamics are first performed in the presence of an inert background gas (Ar) with pressure P = 300 Pa. The initial conditions are set based on the parameterization of the MD results obtained at a delay of 200 ps after the beginning of the laser pulse (100 fs, 800 nm) [16].
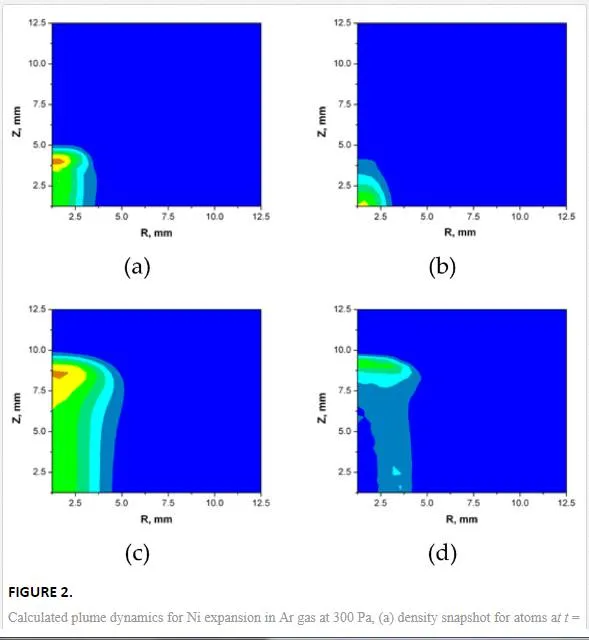
Figure 2 shows separately the density of atoms and clusters for two different delays after the laser pulse. Here, larger clusters were initially at the back of the plume. The obtained results demonstrate that plume front starts experiencing a pronounced deceleration and practically stops at both plume- and gas-dependent delay (here, ~10µs). Theoretically, the initial expansion stage is described by a so-called blast-wave (or, shock-wave) model when shock waves are degenerated.
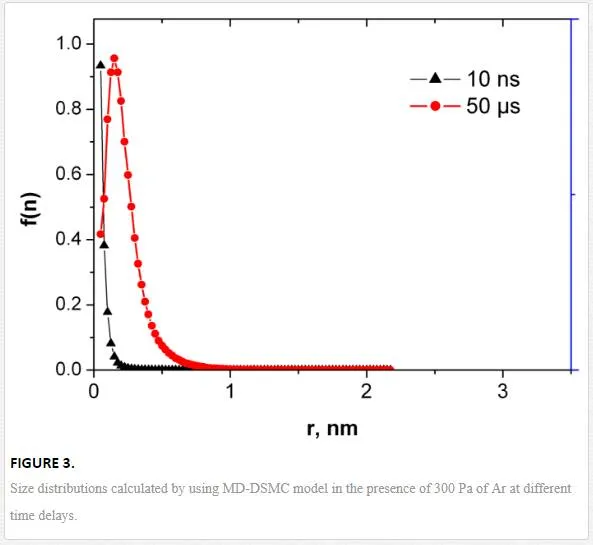
The corresponding nanoparticle size distributions are presented in Figure 3. One can see that after a sufficient delay, a peaked distribution appears instead of a decreasing function. This effect can be explained by collisional growth that is described by the general rate equation having typically log-normal solutions. The amount of sufficiently large nanoparticles formed at such short delays is rather small and cannot explain the finally observed size distributions.
Longer stage includes plume mixing with the background followed by the rapid thermalization and a much more enhanced particle formation. Then, plume species are thermalized and a diffusion-driven regime enters into play.
Spark discharge
In our model developed for spark discharge (SD), the following stages are considered: (i) streamer formation and propagation between electrodes; (ii) streamer-to-spark transition; (iii) gas heating and cylindrical expansion; (iv) electrode evaporation and erosion; (v) nanoparticles formation [16].
Streamer formation is described numerically by using a system of drift-diffusion equations together with Poisson equation for electric potential with a particularly chosen set of boundary conditions. When streamer reaches the opposite electrode, electron emission increases dramatically, so that the streamer is transformed in a conductive plasma column. The oscillations of the electric charge Q in the corresponding circuit with the total resistance RΣ is described by the Kirchhoff’s voltage law.
The oscillating behavior of the discharge is presented in Figure 4, defining the properties of the following plasma column. According to this solution, both electrodes play a role at different delays leading to both evaporation and erosion of the electrodes. When polarity switches, a crater is formed at the surface of one of the electrodes due to both evaporation and erosion.

The erosion flux jΣsurfjsurfΣ is formed due to two main processes: (i) thermal evaporation caused by Joule heating, and (ii) sputtering due to ion bombardment. Similarly to nanosecond laser ablation, evaporation flux jTsurfjsurfT is described by the Hertz-Knudsen equation, where surface temperature is calculated as follows [16]

where s corresponds to the cathode material (solid), c is the specific heat of cathode material, ρs is the density, Ts is the temperature, σs is the electric conductivity, χs is the thermal diffusivity coefficient, k is the Boltzmann constant, α is the sticking coefficient for vapor molecules onto the surface, Peq is the equilibrium vapor pressure, and Psurf is the hydrostatic pressure of gas applied on the surface.
The sputtering yield YY Y and flux jsputsurfjsurfsput is given by

where αsurf is a factor function of m/M, m and M are the atomic weights of cathode material and incident particles, respectively, E+ is the bombarding energy, Usurf is the surface-binding energy, and j+is the flux density of bombarding ions. The solution of Eqs (1–2) yields cathode erosion flow as a function of time. At the same time, plasma column also gains energy by Joule heating.
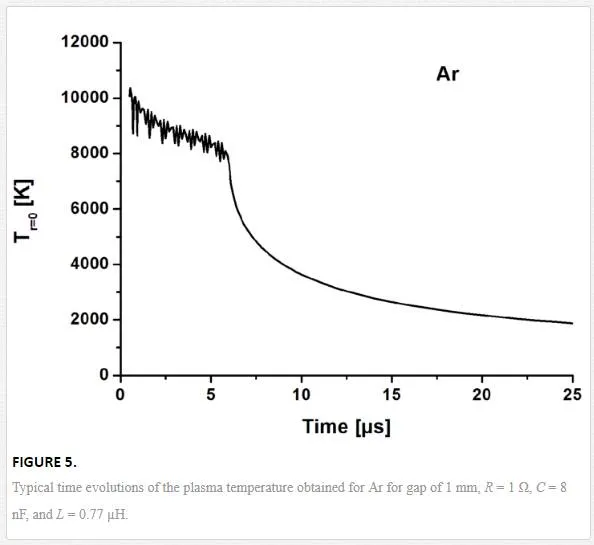
Once the amount of the ejected material is calculated, plasma dynamics is modeled by using Navier-Stokes equations [17]. The corresponding equations contain, in particular, Joule heating term, which determines plasma heating occurring mostly near its axis, where plasma pressure initially arises to several atmospheres. Figure 5 shows typical axial temperature evolution. After a delay of 0.5 µs, which corresponds to plasma expansion, pressure drops back to the values around the atmospheric pressure. Plasma temperature remains high during all the discharging process and drops below electrode boiling point only after 0.1–0.5 ms. During cooling, gas density increases. Lager density and smaller temperature provide conditions required for nanoparticle formation.
Spark discharge vs nanosecond laser ablation
Typically, laser energy absorption leads to the target heating and thermal evaporation in the nanosecond laser ablation of metals. Plasma expansion stage is much longer than the evaporation stage, on the order of ~10 laser pulse temporal widths (~300 ns). Here, plasma electrons gain energy from laser radiation by inverse Bremsstrahlung effect, so that ionization takes place. Then, a so-called blast wave model describes hemispherical expansion as follows [16]:
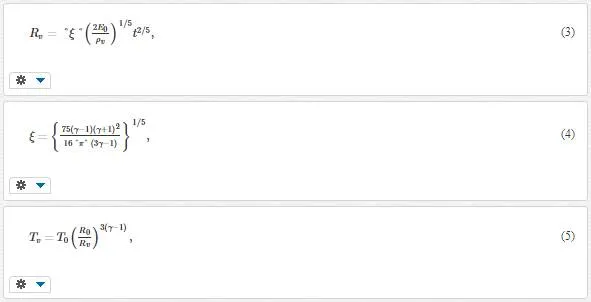
where R0 is the shock wave position, ξ is a constant depending on the plume specific heat capacity, E0 is the initial internal energy of vapor plume, T0 is the initial temperature, and γ is the adiabatic coefficient. This model is valid, if the external shock wave is present and if the mass of the background gas surrounding the shock wave is larger than the mass of the ablated material. During the expansion, both plume temperature and density rapidly decay. As a result, the condition of supersaturation is realized at a certain delay leading to the nanoparticle formation.
Time evolutions of plasma properties are obtained in [16]. For spark discharge, when gas density decreases, plasma resistivity drops down, thus preventing further energy absorption from the electric current. During the expansion, plasma cools down and gas goes back to the axis. These processes are repeated when the energy absorption is high enough for efficient expansion.
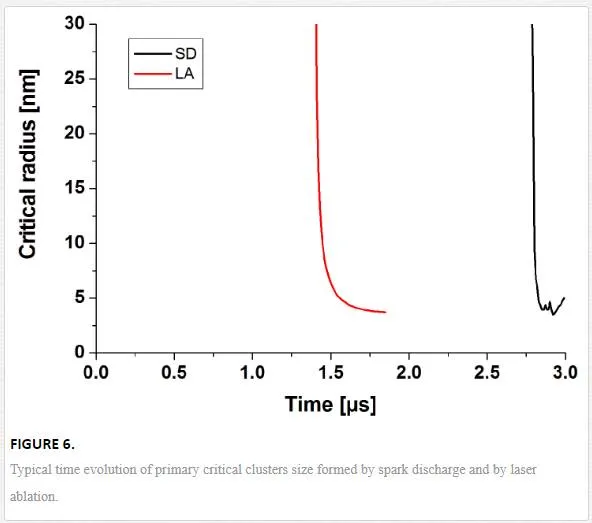
In the case of nanosecond laser ablation, laser energy absorption by the plume takes place. As a result, the ejected plasma is hot, but the energy input is limited in time by laser pulse duration. After the end of the laser pulse, the ablated plume expands and cools down. The critical nuclei sizes are calculated as a function of time (Figure 6).
The obtained results clearly demonstrate that, despite rather different plasma sources, the behavior of particle formation in spark discharge appears to be very similar to the one in laser ablation. The difference in time delays corresponds to the transition of the system to the supersaturated state. Primary NPs formed by nucleation can then evolve due to evaporation, condensation, and/or growth.
Diffusion-driven nucleation leads to the formation of nucleus, whose size is controlled by the free energy as follows [18]:

where k is the Boltzmann constant; T is the temperature in Kelvins; a is the effective radius; ceq is the equilibrium concentration of atoms/monomers; n is the number of atoms/monomers in the nuclei; and
σσ
is the effective surface tension. The peak of the nucleation barrier corresponds to the critical cluster size

As a result, narrow size distributions are produced. The formed particles can collide and aggregate. These collisional processes are described by simplified Smoluchowski equations [18]. Laser-induced fragmentation is neglected here.
Several calculations are performed to study time-evolution of the size distribution for multiple pulse cases. Because saturation is rather high, monomer radius here is as small as a = 1.59–10 and the radius of critical nuclei is recalculated at all the time-steps.
The obtained results (Figure 7) show that when several pulses are applied, these small nuclei grow for pulse number up to 103 because tiny particles grow easier than larger ones. Here, collisions with atoms dominate in the growth process. The obtained results show that further increase in the number of pulses affects particle size distribution only slightly. This effect takes place if laser frequency is not too high, so that the ablated material has time to diffuse and concentration does not grow near the target. As a result, the mean radius can remain rather small (in the nanometer range, smaller than ~3 nm here).
The criterion of the catastrophic nucleation due to thermalization can be derived based on the inequality nc ≤ 1. This means that

The obtained results (Figure 7) show that when several pulses are applied, these small nuclei grow for pulse number up to 103 because tiny particles grow easier than larger ones. Here, collisions with atoms dominate in the growth process. The obtained results show that further increase in the number of pulses affects particle size distribution only slightly. This effect takes place if laser frequency is not too high, so that the ablated material has time to diffuse and concentration does not grow near the target. As a result, the mean radius can remain rather small (in the nanometer range, smaller than ~3 nm here).
The criterion of the catastrophic nucleation due to thermalization can be derived based on the inequality nc ≤ 1. This means that

Typically, at the beginning of the diffusional expansion stage, the condition
ln(S)=ln(c/ceq)=8πa2σ/3kT≥1ln(S)=ln(c/ceq)=8πa2σ/3kT≥1
is valid, so that this mechanism prevails in the nanoparticle formation. Finally, at the last stage, ripening or sintering of the created particles eventually inters into play if the background density is sufficiently high. For instance, this process occurs in liquids, in particular, in the absence of the surface passivation by additional chemicals.
Conclusions
In this chapter, recent advancements in the modeling of laser ablation and spark discharges are summarized. In addition, we have compared processes leading to nanoparticle formation in laser ablation and in spark discharges. In particular, a comparison of the influence of plasma properties on nanoparticle formation has been performed.
First, mechanisms of nanoparticle generation have been investigated for femtosecond laser interactions in the presence of a background environment. The obtained calculation results have demonstrated the long time-evolution of plume species involves nucleation and growth determining the final size distribution that tends to be a limited one with the increase in laser intensity. The obtained results explain several experimental observations including both longer time dynamics of nanoparticles and size distributions. Then, conditions are formulated for catastrophic nucleation to become the main mechanism of nanoparticle formation as a result of thermalization and collisions among the species in the presence of a background environment. The produced nanoparticles can be collected, form a colloid, or can be deposited at a substrate forming nanostructures. Therefore, the presented study is of interest for many applications where both metallic nanoparticles and nanostructures are used in nanophotonics, plasmonics, medicine, biological sensing, textile industry, and other promising fields.
Furthermore, cylindrical plasma column expansion has been shown to govern primary nanoparticle formation in spark discharge, whereas hemispherical shock describes quite well this process for nanosecond laser ablation at atmospheric pressure. In addition, spark discharge leads to oscillations in plasma properties, whereas monotonous behavior is a characteristic for nanosecond laser ablation. Despite the difference in plasma density and time evolutions calculated for both phenomena, after well-defined delays, similar critical nuclei have been shown to be formed by both techniques. This result can be attributed to the fact that whereas larger evaporation rate is typical for nanosecond laser ablation, a mixture of vapor and background gas determines the supersaturation in the case of spark.