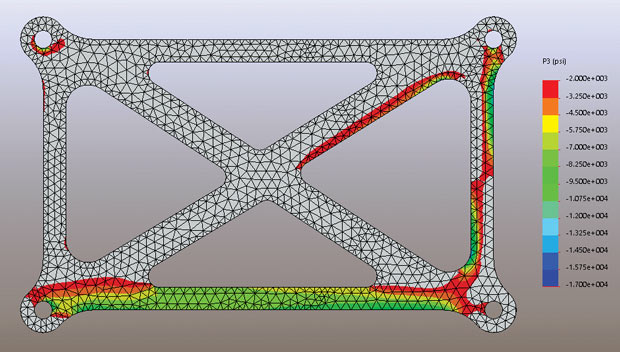
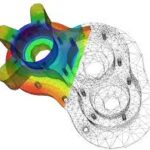
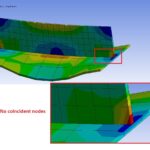
Where does stress come from?  No, I am not talking about your in-laws deciding move in with you for a few months.  I am talking about the stress that you are plotting in those pretty color contour plots for your final report of your static structural finite element analysis for your FEA consulting client. Do you fully understand how those stresses are calculated and displayed by the program?

When we solve a static structural finite element analysis, we are solving the system of equations given by:

{F} = [K] {u}                    

Given the applied loads, the FEA software code calculates the displacements at the nodes.  So how do we get stress from the nodal displacements?   To understand fully, we need to understand how the stiffness matrix is generated.  The stiffness matrix is generated by assembling the stiffness matrices for each individual element.  The stiffness for an individual element comes from the principal of virtual work.  Put simply, the principle of virtual work states that a virtual (very small) change of the internal strain energy must be offset by an identical change in external work due to the applied loads.  The change in strain energy over a volume can be written as:

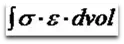
We can replace the stress with the stress-strain relationship:

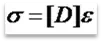
where [D] is the stress-strain matrix and the strain can be replaced with the strain displacement relationship:

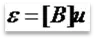
The strain displacement matrix is derived from the element shape functions.  An element shape function defines how the displacements vary through the element.

So, after performing those substitutions, the integral can be expressed as:

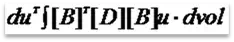
This integral is solved via numerical integration, that is, the terms are evaluated at certain locations in the element, and the total integration is calculated from the evaluation at these locations. These locations are known as the integration points (or Gauss points).

So, back to the calculation of stress from the nodal displacements.  The strains can be calculated from the nodal displacements via the strain-displacement [B] matrix, then the stresses can be calculated from the strains via the stress-strain matrix.  The evaluation of both of these matrices is done only at the integration points that were used to do the integration.  Therefore the strains and stresses are calculated only at the integration points.

But we are usually interested at the stresses at the nodes. Well, there are a couple of options: we can just copy the stresses from the integration points to the nearest nodes, or we can extrapolate the stress from the integration points out to the nodes using an extrapolation function .

Be aware that any kind of material-based stress calculations are done on the integration point level. Things like plasticity, creep, and damage are calculated based on the stresses at the integration points.  Therefore it is possible, in a plasticity analysis, that you can see stresses above yield for an element that shows no plastic straining.  Consider the case where the stress at the integration point is at 99% of yield.  Since it is below yield there is no plastic strain calculated.  Now if we extrapolate the stresses out to the nodes, it is possible that the stress reported at a node is above yield (perhaps the extrapolation gave a stress of 101% of yield).  So you would see a stress above yield but no plastic strain. This is an indication that the mesh may be too coarse.

The next thing that we need to be aware of is that, when reviewing nodal stresses, we are usually looking at average values.  That is, for each element attached to a node, the stress is calculated at the integration points for that element, and then extrapolated (or copied) out to the nodes.  Then, the nodal value of stress is the average of all the elemental stress values connected to that node. 

As the mesh is refined, these differences will become smaller (assuming that there is not a true stress discontinuity at this location). Therefore the difference between average and unaveraged stresses at a node is one indication of an adequate mesh density.

So, you see that there are a lot of steps to go through to derive nodal stresses from the calculated nodal displacements. Just blindly reporting averaged nodal stresses without understanding what goes into deriving those stress values is like saying to your in-laws, “sure, stay as long as you’d like”.