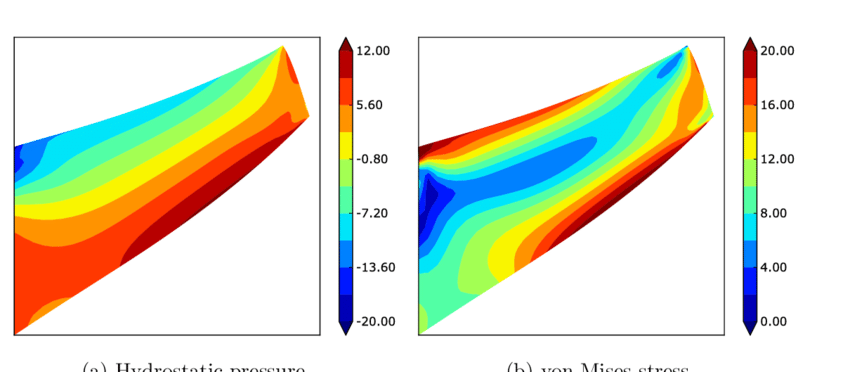
If you have ever tried to model the structural behavior of an elastomer using finite element analysis as part of your FEA consulting projects, you may have experienced the painful process of trying to obtain a converged solution. Elastomers are materials such as natural and synthetic rubbers that can undergo large elastic deformations of 100-700%, typically have highly nonlinear stress-strain behavior, and are nearly incompressible. All of these features can cause headaches with your finite element analysis convergence, but for now let’s focus on incompressibility.
An incompressible or nearly incompressible material does not change volume during deformation, and will have a Poisson’s ratio tending or equal to 0.5. Consider the principal state of stress for an infinitesimal element, which can be separated into hydrostatic stress and deviatoric stress:
 |
Hydrostatic stress causes volume change only, whereas deviatoric stress causes angular distortion only. The hydrostatic pressure, p, is the product of the bulk modulus of the material (K) and the volumetric strain 
 |
For an incompressible or nearly incompressible material, one can clearly see that K tends to infinity as the Poisson’s ratio tends to 0.5, and the volumetric strain i by definition tending to zero. These conditions will result in numerical difficulties, and can exhibit overly stiff behavior caused by volumetric locking.
A number of element formulations are available to help address the numerical issues caused by incompressibility. In ANSYS, the KEYOPT command is used to control and set the element formulations. These settings will typically require inserting a Command Block within ANSYS Mechanical. Following is a brief review of some of the most useful:
1. Selective reduced integration (B-Bar)
The B-bar method uses an integration rule one order lower for volumetric terms, allowing it to act “softer” since it is not fully integrated, overcoming volumetric locking. It is known as the B-bar method because B, the strain-displacement matrix, is averaged on the volume term, i.e. 
2. Uniform reduced integration (URI)
Both volumetric and deviatoric terms use an integration rule one order lower than full integration. URI is efficient in that less CPU time is required for element calculations and file sizes are reduced. Unfortunately, for lower order elements, reduced integration of deviator terms can cause modes of deformation which have zero strain energy, called hourglass modes, that lead to physically unrealistic behavior (see figure below). An hourglass stiffness factor is typically available for these elements to help eliminate the hourglass modes. If required, the user must check to see that the artificial energy due to hourglass control stiffness is a small (< 5%) percentage of the total stiffness energy.
 |

In ANSYS, the hourglass stiffness factor is defined using REAL constant HGSTF, the artificial energy can be plotted using PLESOL,AENE, and the total stiffness energy using PLESOL,SENE.
3. Enhanced Strain Formulation
This formulation adds internal degrees of freedom to lower-order hex/quads. It is designed to “soften” the bending response, and can improve behavior in nearly incompressible applications. However, it should not be used alone for fully incompressible analysis, and instead should be combined with Mixed u-P formulation (discussed next).
4. Mixed u-P Formulation
Mixed u-P formulation is used to treat volumetric locking by solving hydrostatic pressure (i.e. volumetric strain) as an additional degree of freedom. It can be combined with B-bar, URI and Enhanced Strain formulations. Because the pressure terms are kept in the assembled stiffness matrix, the stiffness matrix is unsymmetric. Thus, only direct solvers can be used with this option due to the ill-conditioned matrix.
ANSYS, by default, uses a technique where it creates an equivalent symmetric stiffness matrix to represent the unsymmetric matrix. An unsymmetric solver can be invoked using the NROPT,UNSYM command, which has been found to provide better convergence behavior in some cases. Also, if using Mixed u-P formulation, an additional convergence criterion is added based on the volumetric compatibility condition. The default tolerance for this criterion can sometimes be severe, and it can be changed using the fourth entry on the SOLCONTROL command.
Summary
There are many different technologies for continuum elements to alleviate volumetric locking that is often found in incompressible or nearly incompressible materials. Although there is no one perfect approach, there are usually a number of options that can be used. Since these options are not necessarily default options, an understanding of incompressibility is essential for obtaining robust converged solutions as part of your FEA consulting projects.