Refraction is the bending of the path of a light wave as it passes across the boundary separating two media. Refraction is caused by the change in speed experienced by a wave when it changes medium. Lesson 1, focused on the topics of “What causes refraction?” and “Which direction does light refract?” In that lesson, we learned that light can either refract towards the normal (when slowing down while crossing the boundary) or away from the normal (when speeding up while crossing the boundary). The focus of Lesson 2 is upon the question of “By how much does light refract when it crosses a boundary?” In the first part of Lesson 2, we learned that a comparison of the angle of refraction to the angle of incidence provides a good measure of the refractive ability of any given boundary. The more that light refracts, the bigger the difference between these two angles. In this part of Lesson 2, we will learn about a mathematical equation relating these two angles and the indices of refraction of the two materials on each side of the boundary.
 A Lesson from the Laboratory
A Lesson from the Laboratory
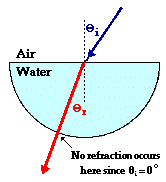
To begin, consider a hemi-cylindrical dish filled with water. Suppose that a laser beam is directed towards the flat side of the dish at the exact center of the dish. The angle of incidence can be measured at the point of incidence. This ray will refract, bending towards the normal (since the light is passing from a medium in which it travels fast into one in which it travels slow – FST). Once the light ray enters the water, it travels in a straight line until it reaches the second boundary. At the second boundary, the light ray is approaching along the normal to the curved surface (this stems from the geometry of circles). The ray does not refract upon exiting since the angle of incidence is 0-degrees (recall the If I Were An Archer Fish page). The ray of laser light therefore exits at the same angle as the refracted ray of light made at the first boundary. These two angles can be measured and recorded. The angle of incidence of the laser beam can be changed to 5-degrees and new measurements can be made and recorded. This process can be repeated until a complete data set of accurate values has been collected. The data below show a representative set of data for such an experiment.
| Angle of Incidence (degrees) | Angle of Refraction (degrees) |
| 0.00 | 0.00 |
| 5.00 | 3.8 |
| 10.0 | 7.5 |
| 15.0 | 11.2 |
| 20.0 | 14.9 |
| 25.0 | 18.5 |
| 30.0 | 22.1 |
| 35.0 | 25.5 |
| 40.0 | 28.9 |
| 45.0 | 32.1 |
| 50.0 | 35.2 |
| 55.0 | 38.0 |
| 60.0 | 40.6 |
| 65.0 | 43.0 |
| 70.0 | 45.0 |
| 75.0 | 46.6 |
| 80.0 | 47.8 |
| 85.0 | 48.5 |
An inspection of the data above reveals that there is no clear linear relationship between the angle of incidence and the angle of refraction. For example, a doubling of the angle of incidence from 40 degrees to 80 degrees does not result in a doubling of the angle of refraction. Thus, a plot of this data would not yield a straight line. If however, the sine of the angle of incidence and the sine of the angle of refraction were plotted, the plot would be a straight line, indicating a linear relationship between the sines of the important angles. If two quantities form a straight line on a graph, then a mathematical relationship can be written in y = m*x + b form. A plot of the sine of the angle of incidence vs. the sine of the angle of refraction is shown below.
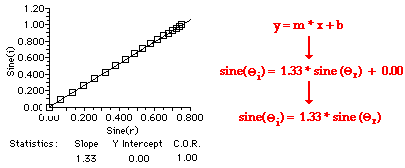
The equation relating the angles of incidence (Θi) and the angle of refraction (Θr) for light passing from air into water is given as
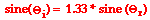
Observe that the constant of proportionality in this equation is 1.33 – the index of refraction value of water. Perhaps it’s just a coincidence. But if the semi-cylindrical dish full of water was replaced by a semi-cylindrical disk of Plexiglas, the constant of proportionality would be 1.51 – the index of refraction value of Plexiglas. This is not just a coincidence. The same pattern would result for light traveling from air into any material. Experimentally, it is found that for a ray of light traveling from air into some material, the following equation can be written.

where nmaterial = index of refraction of the material
This study of the refraction of light as it crosses from one material into a second material yields a general relationship between the sines of the angle of incidence and the angle of refraction. This general relationship is expressed by the following equation:
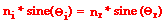
where Θi (“theta i”) = angle of incidence
Θr (“theta r”) = angle of refraction
ni = index of refraction of the incident medium
nr = index of refraction of the refractive medium
This relationship between the angles of incidence and refraction and the indices of refraction of the two media is known as Snell’s Law. Snell’s law applies to the refraction of light in any situation, regardless of what the two media are.
Using Snell’s Law to Predict An Angle Value
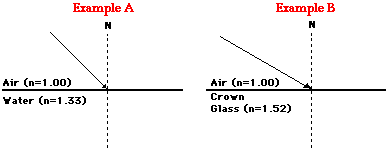
As with any equation in physics, the Snell’s Law equation is valued for its predictive ability. If any three of the four variables in the equation are known, the fourth variable can be predicted if appropriate problem-solving skills are employed. This is illustrated in the two examples below.
In each of these two example problems, the angle of refraction is the variable to be determined. The indices of refraction (ni and nr) are given and the angle of incidence can be measured. With three of the four variables known, substitution into Snell’s law followed by algebraic manipulation will lead to the answer.
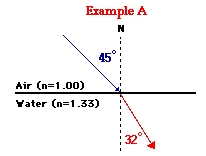
Solution to Example A
First, use a protractor to measure the angle of incidence. An appropriate measurement would be some angle close to 45-degrees.
Second, list all known values and the unknown value for which you wish to solve:
| Given:ni = 1.00 | Find:Θr = ??? |
Third, list the relevant equation:
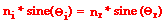
Fourth, substitute known values into the equation and algebraically manipulate the equation in order to solve for the unknown variable – Θr.
1.00 * sine (45 degrees) = 1.33 * sine (Θr)
0.7071 = 1.33 * sine (Θr)
0.532 = sine (Θr)
sine-1 (0.532) = sine-1 ( sine Θr)
32.1 degrees = Θr
Proper algebra yields to the answer of 32.1 degrees for the angle of refraction. The diagram showing the refracted ray can be viewed by clicking the View Diagram button below.
View Diagram

![]() The solution to Example A is given as an example. Try Example B on your own and click on the See Answer button to check your answer.
The solution to Example A is given as an example. Try Example B on your own and click on the See Answer button to check your answer.
See Answer

Answer: 34.7 degrees
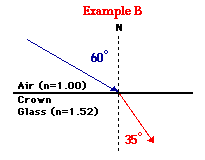
Measure the angle of incidence – the angle between the normal and incident ray. It is approximately 60 degrees.
List known Values:
ni =1.00
nr =1.52
Theta i = 60 degrees
List Unknown: Find theta r
Substitute into Snell’s law equation and perform the necessary algebraic operations to solve:
1.00 • sine(60 degrees) = 1.52 • sine(theta r)
0.8660 = 1.52 • sine(theta r)
0.570 = sine(theta r)
34.7 degrees = theta r
Now draw the refracted ray at an angle of 34.7 degrees from the normal – see diagram below.
Snell’s Law provides the quantitative means of answering the question of “By how much does the light ray refract?” The task of answering this question involves using indices of refraction and the angle of incidence values in order to determine the angle of refraction. This problem-solving process is discussed in more detail on the remaining pages of Lesson 2.
Flickr Physics Photo
Laser light is shown passing into and out of a hemi-cylindrical dish filled with water. The light enters the water (at the curved side of the dish) along the normal line; no bending occurs upon entry. The light continues through the water along a straight line until it reaches the boundary with air (at the flat side of the dish). The angle of incidence in the water is approximately 39°. At this angle, the light refracts out of the water into the surrounding air bending away from the normal. The angle of refraction in the air is approximately 57°. These values for the angle of incidence and refraction are consistent with Snell’s Law.