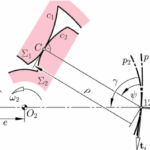
Involute Profile
The following examples are involute spur gears. We use the word involute because the contour of gear teeth curves inward. Gears have many terminologies, parameters and principles. One of the important concepts is the velocity ratio, which is the ratio of the rotary velocity of the driver gear to that of the driven gears.
Generation of the Involute Curve
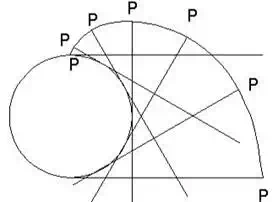
| The curve most commonly used for gear-tooth profiles is the involute of a circle. This involute curve is the path traced by a point on a line asthe line rolls without slipping on the circumference of a circle. It may also be defined as a path traced by the end of a string, which is originally wrapped on a circle when the string is unwrapped from the circle. The circle from which the involute is derived is called the base circle. | |
| The involute profile of gears has important | Involute curve |
| advantages; | |
1. It is easy to manufacture and the centre distance between a pair of involute gears can be varied without changing the velocity ratio. Thus close tolerances between shaft locations are not required. The most commonly used conjugate tooth curve is the involute curve.
2. In involute gears, the pressure angle, remains constant between the point of tooth engagement and disengagement. It is necessary for smooth running and less wear of gears.
3. The face and flank of involute teeth are generated by a single curve where as in cycloidal gears, double curves (i.e. epi-cycloid and hypo-cycloid) are required for the face and flank respectively. Thus the involute teeth are easy to manufacture than cycloidal teeth.
In involute system, the basic rack has straight teeth and the same can be cut with simple tools.
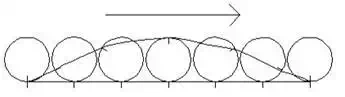
Cycloidal profile:
A cycloid is the curve traced by a point on the circumference of a circle which rolls without slipping on a fixed straight line. When a circle rolls without slipping on the outside of a fixed circle, the curve traced by a point on the circumference of a circle is known as epi-cycloid. On the other hand, if a circle rolls without slipping on the by a point on the circumference of a circle is inside of a fixed circle, then the curve traced hypo-cycloid.