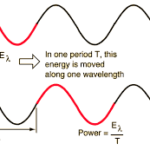
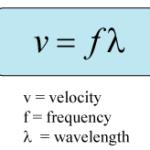
A wave is a disturbance that moves along a medium from one end to the other. If one watches an ocean wave moving along the medium (the ocean water), one can observe that the crest of the wave is moving from one location to another over a given interval of time. The crest is observed to cover distance. The speed of an object refers to how fast an object is moving and is usually expressed as the distance traveled per time of travel. In the case of a wave, the speed is the distance traveled by a given point on the wave (such as a crest) in a given interval of time. In equation form,
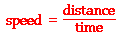
If the crest of an ocean wave moves a distance of 20 meters in 10 seconds, then the speed of the ocean wave is 2.0 m/s. On the other hand, if the crest of an ocean wave moves a distance of 25 meters in 10 seconds (the same amount of time), then the speed of this ocean wave is 2.5 m/s. The faster wave travels a greater distance in the same amount of time.
Sometimes a wave encounters the end of a medium and the presence of a different medium. For example, a wave introduced by a person into one end of a slinky will travel through the slinky and eventually reach the end of the slinky and the presence of the hand of a second person. One behavior that waves undergo at the end of a medium is reflection. The wave will reflect or bounce off the person’s hand. When a wave undergoes reflection, it remains within the medium and merely reverses its direction of travel. In the case of a slinky wave, the disturbance can be seen traveling back to the original end. A slinky wave that travels to the end of a slinky and back has doubled its distance. That is, by reflecting back to the original location, the wave has traveled a distance that is equal to twice the length of the slinky.
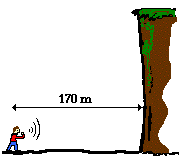Reflection phenomena are commonly observed with sound waves. When you let out a hollerwithin a canyon, you often hear the echo of the holler. The sound wave travels through the medium (air in this case), reflects off the canyon wall and returns to its origin (you). The result is that you hear the echo (the reflected sound wave) of your holler. A classic physics problem goes like this:
Noah stands 170 meters away from a steep canyon wall. He shouts and hears the echo of his voice one second later. What is the speed of the wave?
In this instance, the sound wave travels 340 meters in 1 second, so the speed of the wave is 340 m/s. Remember, when there is a reflection, the wave doubles its distance. In other words, the distance traveled by the sound wave in 1 second is equivalent to the 170 meters down to the canyon wall plus the 170 meters back from the canyon wall.
Variables Affecting Wave Speed
What variables affect the speed at which a wave travels through a medium? Does the frequency or wavelength of the wave affect its speed? Does the amplitude of the wave affect its speed? Or are other variables such as the mass density of the medium or the elasticity of the medium responsible for affecting the speed of the wave? These questions are often investigated in the form of a lab in a physics classroom.
Suppose a wave generator is used to produce several waves within a rope of a measurable tension. The wavelength, frequency and speed are determined. Then the frequency of vibration of the generator is changed to investigate the effect of frequency upon wave speed. Finally, the tension of the rope is altered to investigate the effect of tension upon wave speed. Sample data for the experiment are shown below.
Speed of a Wave Lab – Sample Data
| Trial | Tension (N) | Frequency (Hz) | Wavelength (m) | Speed (m/s) |
| 1 | 2.0 | 4.05 | 4.00 | 16.2 |
| 2 | 2.0 | 8.03 | 2.00 | 16.1 |
| 3 | 2.0 | 12.30 | 1.33 | 16.4 |
| 4 | 2.0 | 16.2 | 1.00 | 16.2 |
| 5 | 2.0 | 20.2 | 0.800 | 16.2 |
| 6 | 5.0 | 12.8 | 2.00 | 25.6 |
| 7 | 5.0 | 19.3 | 1.33 | 25.7 |
| 8 | 5.0 | 25.5 | 1.00 | 25.5 |
In the first five trials, the tension of the rope was held constant and the frequency was systematically changed. The data in rows 1-5 of the table above demonstrate that a change in the frequency of a wave does not affect the speed of the wave. The speed remained a near constant value of approximately 16.2 m/s. The small variations in the values for the speed were the result of experimental error, rather than a demonstration of some physical law. The data convincingly show that wave frequency does not affect wave speed. An increase in wave frequency caused a decrease in wavelength while the wave speed remained constant.
The last three trials involved the same procedure with a different rope tension. Observe that the speed of the waves in rows 6-8 is distinctly different than the speed of the wave in rows 1-5. The obvious cause of this difference is the alteration of the tension of the rope. The speed of the waves was significantly higher at higher tensions. Waves travel through tighter ropes at higher speeds. So while the frequency did not affect the speed of the wave, the tension in the medium (the rope) did. In fact, the speed of a wave is not dependent upon (causally affected by) properties of the wave itself. Rather, the speed of the wave is dependent upon the properties of the medium such as the tension of the rope.
One theme of this unit has been that “a wave is a disturbance moving through a medium.” There are two distinct objects in this phrase – the “wave” and the “medium.” The medium could be water, air, or a slinky. These media are distinguished by their properties – the material they are made of and the physical properties of that material such as the density, the temperature, the elasticity, etc. Such physical properties describe the material itself, not the wave. On the other hand, waves are distinguished from each other by their properties – amplitude, wavelength, frequency, etc. These properties describe the wave, not the material through which the wave is moving. The lesson of the lab activity described above is that wave speed depends upon the medium through which the wave is moving. Only an alteration in the properties of the medium will cause a change in the speed.
Check Your Understanding
1. A teacher attaches a slinky to the wall and begins introducing pulses with different amplitudes. Which of the two pulses (A or B) below will travel from the hand to the wall in the least amount of time? Justify your answer.
See Answer
They reach the wall at the same time. Don’t be fooled! The amplitude of a wave does not affect the speed at which the wave travels. Both Wave A and Wave B travel at the same speed. The speed of a wave is only altered by alterations in the properties of the medium through which it travels.
2. The teacher then begins introducing pulses with a different wavelength. Which of the two pulses (C or D) will travel from the hand to the wall in the least amount of time ? Justify your answer.
See Answer
They reach the wall at the same time. Don’t be fooled! The wavelength of a wave does not affect the speed at which the wave travels. Both Wave C and Wave D travel at the same speed. The speed of a wave is only altered by alterations in the properties of the medium through which it travels.
3. The time required for the sound waves (v = 340 m/s) to travel from the tuning fork to point A is ____ .
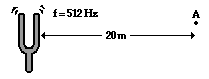
| a. 0.020 second | b. 0.059 second |
| c. 0.59 second | d. 2.9 second |
See Answer
Answer: B
GIVEN: v = 340 m/s, d = 20 m and f = 1000 Hz
Find time
Use v = d / t and rearrange to t = d / v
Substitute and solve.
4. Two waves are traveling through the same container of nitrogen gas. Wave A has a wavelength of 1.5 m. Wave B has a wavelength of 4.5 m. The speed of wave B must be ________ the speed of wave A.
| a. one-ninth | b. one-third |
| c. the same as | d. three times larger than |
See Answer
Answer: C
The medium is the same for both of these waves (“the same container of nitrogen gas”). Thus, the speed of the wave will be the same. Alterations in a property of a wave (such as wavelength) will not affect the speed of the wave. Two different waves travel with the same speed when present in the same medium.
5. An automatic focus camera is able to focus on objects by use of an ultrasonic sound wave. The camera sends out sound waves that reflect off distant objects and return to the camera. A sensor detects the time it takes for the waves to return and then determines the distance an object is from the camera. The camera lens then focuses at that distance. Now that’s a smart camera! In a subsequent life, you might have to be a camera; so try this problem for practice:
If a sound wave (speed = 340 m/s) returns to the camera 0.150 seconds after leaving the camera, then how far away is the object?
See Answer
GIVEN: v = 340 m/s, t = 0.150 s (down and back time)
Find d (1-way)
If it takes 0.150 s to travel to the object and back, then it takes 0.075 s to travel the one-way distance to the object. Now solve for time using the equation d = v • t.
d = v • t = (340 m/s) • (0.075 s) = 25.5 m
6. TRUE or FALSE:
Doubling the frequency of a wave source doubles the speed of the waves.
See Answer
FALSE!
The speed of a wave is unaffected by changes in the frequency.
7. While hiking through a canyon, Noah Formula lets out a scream. An echo (reflection of the scream off a nearby canyon wall) is heard 0.82 seconds after the scream. The speed of the sound wave in air is 342 m/s. Calculate the distance from Noah to the nearby canyon wall.
See Answer
GIVEN: v = 342 m/s, t = 0.82 s (2-way)
Find d (1-way)
If it takes 0.82 s to travel to the canyon wall and back (a down-and-back time), then it takes 0.41 s to travel the one-way distance to the wall. Now use d = v • t
d = v • t = (342 m/s) • (0.41 s) = 140 m
8. Mac and Tosh are resting on top of the water near the end of the pool when Mac creates a surface wave. The wave travels the length of the pool and back in 25 seconds. The pool is 25 meters long. Determine the speed of the wave.
See Answer
GIVEN: d (1-way) =25 m, t (2-way)=25 s
Find v.
If the pool is 25 meters long, then the back-and-forth distance is 50 meters. The wave covers this distance in 25 seconds. Now use v = d / t.
v = d / t = (50 m) / (25 s) = 2 m/s
9. The water waves below are traveling along the surface of the ocean at a speed of 2.5 m/s and splashing periodically against Wilbert’s perch. Each adjacent crest is 5 meters apart. The crests splash Wilbert’s feet upon reaching his perch. How much time passes between each successive drenching? Answer and explain using complete sentences.
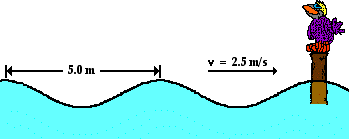
See Answer
If the wave travels 2.5 meters in one second then it will travel 5.0 meters in 2.0 seconds. If Wilbert gets drenched every time the wave has traveled 5.0 meters, then he will get drenched every 2.0 seconds.
