We have previously shown in Lesson 4 that any charged object – positive or negative, conductor or insulator – creates an electric field that permeates the space surrounding it. In the case of conductors there are a variety of unusual characteristics about which we could elaborate. Recall from Lesson 1 that a conductor is material that allows electrons to move relatively freely from atom to atom. It was emphasized that when a conductor acquires an excess charge, the excess charge moves about and distributes itself about the conductor in such a manner as to reduce the total amount of repulsive forces within the conductor. We will explore this in more detail in this section of Lesson 4 as we introduce the idea of electrostatic equilibrium. Electrostatic equilibrium is the condition established by charged conductors in which the excess charge has optimally distanced itself so as to reduce the total amount of repulsive forces. Once a charged conductor has reached the state of electrostatic equilibrium, there is no further motion of charge about the surface.

Electric Fields Inside of Charged Conductors

Charged conductors that have reached electrostatic equilibrium share a variety of unusual characteristics. One characteristic of a conductor at electrostatic equilibrium is that the electric field anywhere beneaththe surface of a charged conductor is zero. If an electric field did exist beneath the surface of a conductor (and inside of it), then the electric field would exert a force on all electrons that were present there. This net force would begin to accelerate and move these electrons. But objects at electrostatic equilibrium have no further motion of charge about the surface. So if this were to occur, then the original claim that the object was at electrostatic equilibrium would be a false claim. If the electrons within a conductor have assumed an equilibrium state, then the net force upon those electrons is zero. The electric field lines either begin or end upon a charge and in the case of a conductor, the charge exists solely upon its outer surface. The lines extend from this surface outward, not inward. This of course presumes that our conductor does not surround a region of space where there was another charge.

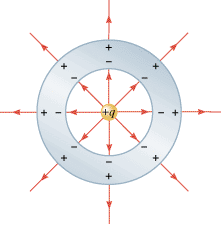
To illustrate this characteristic, let’s consider the space between and inside of two concentric, conducting cylinders of different radii as shown in the diagram at the right. The outer cylinder is charged 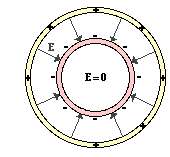positively. The inner cylinder is charged negatively. The electric field about the inner cylinder is directed towards the negatively charged cylinder. Since this cylinder does not surround a region of space where there is another charge, it can be concluded that the excess charge resides solely upon the outer surface of this inner cylinder. The electric field inside the inner cylinder would be zero. When drawing electric field lines, the lines would be drawn from the inner surface of the outer cylinder to the outer surface of the inner cylinder. For the excess charge on the outer cylinder, there is more to consider than merely the repulsive forces between charges on its surface. While the excess charge on the outer cylinder seeks to reduce repulsive forces between its excess charge, it must balance this with the tendency to be attracted to the negative charges on the inner cylinder. Since the outer cylinder surrounds a region that is charged, the characteristic of charge residing on the outer surface of the conductor does not apply.

This concept of the electric field being zero inside of a closed conducting surface was first demonstrated by Michael Faraday, a 19th century physicist who promoted the field theory of electricity. Faraday constructed a room within a room, covering the inner room with a metal foil. He sat inside the inner room with an electroscope and charged the surfaces of the outer and inner room using an electrostatic generator. While sparks were seen flying between the walls of the two rooms, there was no detection of an electric field within the inner room. The excess charge on the walls of the inner room resided entirely upon the outer surface of the room. Today, this demonstration is often repeated in physics demonstration shows at museums and universities.

The inner room with the conducting frame that protected Faraday from the static charge is now referred to as a Faraday’s cage. The cage serves to shield whomever and whatever is on the inside from the influence of electric fields. Any closed, conducting surface can serve as a Faraday’s cage, shielding whatever it surrounds from the potentially damaging effects of electric fields. This principle of shielding is commonly utilized today as we protect delicate electrical equipment by enclosing them in metal cases. Even delicate computer chips and other components are shipped inside of conducting plastic packaging that shields the chips from potentially damaging effects of electric fields. This is one more example of “Physics for Better Living.”

Electric Fields are Perpendicular to Charged Surfaces

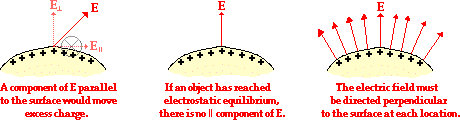
A second characteristic of conductors at electrostatic equilibrium is that the electric field upon the surface of the conductor is directed entirely perpendicular to the surface. There cannot be a component of electric field (or electric force) that is parallel to the surface. If the conducting object is spherical, then this means that the perpendicular electric field vectors are aligned with the center of the sphere. If the object is irregularly shaped, then the electric field vector at any location is perpendicular to a tangent line drawn to the surface at that location.

Understanding why this characteristic is true demands an understanding of vectors, force and motion. The motion of electrons, like any physical object, is governed by Newton’s laws. One outcome of Newton’s laws was that unbalanced forces cause objects to accelerate in the direction of the unbalanced force and a balance of forces causes objects to remain at equilibrium. This truth provides the foundation for the rationale behind why electric fields must be directed perpendicular to the surface of conducting objects. If there were a component of electric field directed parallel to the surface, then the excess charge on the surface would be forced into accelerated motion by this component. If a charge is set into motion, then the object upon which it is on is not in a state of electrostatic equilibrium. Therefore, the electric field must be entirely perpendicular to the conducting surface for objects that are at electrostatic equilibrium. Certainly a conducting object that has recently acquired an excess charge has a component of electric field (and electric force) parallel to the surface; it is this component that acts upon the newly acquired excess charge to distribute the excess charge over the surface and establish electrostatic equilibrium. But once reached, there is no longer any parallel component of electric field and no longer any motion of excess charge.

Electric Fields and Surface Curvature

A third characteristic of conducting objects at electrostatic equilibrium is that the electric fields are strongest at locations along the surface where the object is most curved. The curvature of a surface can range from absolute flatness on one extreme to being curved to a blunt point on the other extreme.

A flat location has no curvature and is characterized by relatively weak electric fields. On the other hand, ablunt point has a high degree of curvature and is characterized by relatively strong electric fields. A sphere is uniformly shaped with the same curvature at every location along its surface. As such, the electric field strength on the surface of a sphere is everywhere the same.

To understand the rationale for this third characteristic, we will consider an irregularly shaped object that is negatively charged. Such an object has an excess of electrons. These electrons would distribute themselves in such a manner as to reduce the effect of their repulsive forces. Since 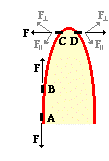electrostatic forces vary inversely with the square of the distance, these electrons would tend to position themselves so as to increase their distance from one another. On a regularly shaped sphere, the ultimate distance between every neighboring electron would be the same. But on an irregularly shaped object, excess electrons would tend to accumulate in greater density along locations of greatest curvature. Consider the diagram at the right. Electrons A and B are located along a flatter section of the surface. Like all well-behaved electrons, they repel each other. The repulsive forces are directed along a line connecting charge to charge, making the repulsive force primarily parallel to the surface. On the other hand, electrons C and D are located along a section of the surface with a sharper curvature. These excess electrons also repel each other with a force directed along a line connecting charge to charge. But now the force is directed at a sharper angle to the surface. The components of these forces parallel to the surface are considerably less. A majority of the repulsive force between electrons C and D is directed perpendicular to the surface.

The parallel components of these repulsive forces are what cause excess electrons to move along the surface of the conductor. The electrons will move and distribute themselves until electrostatic equilibrium is reached. Once reached, the resultant of all parallel components on any given excess electron (and on all excess electrons) will add up to zero. All the parallel components of force on each of the electrons must be zero since the net force parallel to the surface of the conductor is always zero (the second characteristicdiscussed above). For the same separation distance, the parallel component of force is greatest in the case of electrons A and B. So to acquire this balance of parallel forces, electrons A and B must distance themselves further from each other than electrons C and D. Electrons C and D on the other hand can crowd closer together at their location since that the parallel component of repulsive forces is less. In the end, a relatively large quantity of charge accumulates on the locations of greatest curvature. This larger quantity of charge combined with the fact that their repulsive forces are primarily directed perpendicular to the surface results in a considerably stronger electric field at such locations of increased curvature.

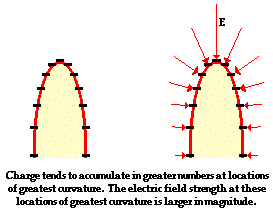
The fact that surfaces that are sharply curved to a blunt edge create strong electric fields is the underlying principle for the use of lightning rods. In the next section of Lesson 4, we will explore the phenomenon of lightning discharge and the use of lightning rods to prevent lightning strikes.
 

 

Check Your Understanding

Use your understanding to answer the following questions. When finished, click the button to view the answers.

1. Suppose that the sphere of a Van de Graaff generator gathers a charge. Then the motor is turned off and the sphere is allowed to reach electrostatic equilibrium. The charge ___.

a. resides both on its surface and throughout its volume

b. resides mostly inside the sphere and only emerges outside when touched

c. resides only on the surface of the sphere

See Answer

Answer: C

When a “closed” conductor becomes charged, the excess of charge accumulates on the outer surface of the conductor. Since the generator has been turned off, there is no source of charge inside of it. All the charge resides on the outside of the dome.

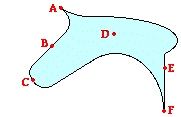2. Describe the electric field strength at the six labeled locations of the irregularly shaped charged object at the right. Use the phrases “zero,” “relatively weak,” “moderate,” and relatively strong” as your descriptions.

See Answer

Answers:

A, F are relatively strong since they’re the most pointed locations on the conductor’s surface.

B, E are relatively weak since they’re at the least curved (most flat) locations on the conductor’s surface.

C is of moderate strength since it is at a location with some curvature but not an extreme amount.

D is 0 since it is at a location under the surface of the conductor; electric fields are zero inside of conductors.

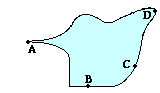3. A diagram of an irregularly shaped charged conductor is shown at the right. Four locations along the surface are labeled – A, B, C, and D. Rank these locations in increasing order of the strength of their electric field, beginning with the smallest electric field.

See Answer

Answer: B < C < D < A

For conducting surfaces, electric fields are strongest at locations where the curvature is the greatest. A projection (such as at point A) is the extreme case of lots of curvature. A flat section of a surface (such as point B) is on the opposite extreme with with no curvature. So point B is listed first and point A is listed last. Since point D is on a section of the surface which curves more than point C’s section, the ordering of the final two locations is point C < point D.

4. Consider the diagram of the thumbtack shown at the right. Suppose that the thumbtack becomes positively charged. Draw the electric field lines surrounding the thumbtack.

See electric field line diagram.

5. Diagram the electric field lines for the following configuration of two objects. Place arrows on your field lines.

6. A favorite physics demonstration used with the Van de Graaff generator involves slowly approaching the dome holding a paper clip stretched towards the device. Why does the demonstrator not become toast when approaching the machine with the blunt edge of the paper clip protruding forward?

See Answer

Answer:

An uncoiled paper clip becomes an object with a blunt edge with extreme curvature at its tip. This extreme curvature creates strong electric fields around its surface. The strength of the electric field is great enough to ionize the air between the paper clip and the Van de Graaff dome. This provides a conducting path from the dome to the clip. Charge that normally accumulates on the dome now flows through the ionized air and is grounded through the demonstrator. Rather than experiencing a sudden discharge of large quantities of charge, there is a gradual non-harmful (so he claims) flow of charge off the dome.

7. TRUE or FALSE:

Lightning rods are placed on homes to protect them from lightning. They work because the electric field is weak around the lightning rods; thus, there is little flow of charge between the lightning rods/home and the charged clouds.

See Answer

Answer: False

Electric fields are very strong along the sharply curved or blunt edges of lightning rod. This creates strong electric fields. To find out why they prevent lightning strikes, you’ll have to read the next section of Lesson 4.

Electric Field Line Diagram for Question #4:

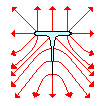
The above diagram was not created by a Field Plotting software program; it would certainly look better if it had been. Your answer may look different (especially when the details are compared) but it should share the following general characteristics with the diagram given here:

·         The electric field lines should be directed from the positively charged thumbtack to the extremities of the page. Each field line MUST have an arrowhead on it to indicate such directions.

·         All electric field lines should be perpendicular to the surface of the thumbtack at the locations where the lines and the thumbtack meet.

·         There should be more lines concentrated at the pointed extremity of the thumbtack and the two sharply curved sections and fewer lines along the flatter sections of the thumbtack.

Return to Question #4

Electric Field Line Diagram for Question #5:

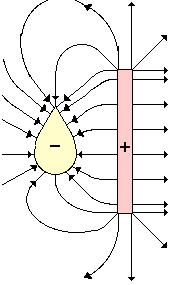
Once more, the above diagram was not created by a Field Plotting software program; it would likely look better if it had been. Your answer may look different (especially when the details are compared) but it should share the following general characteristics with the diagram given here:

·         The field lines should be directed from + to – or from the edge of the page to the – or from + to the edge of the page. Each field line MUST have an arrowhead on it to indicate such directions.

·         At the surface of either object, the field lines should be directed perpendicular to the surface.

·         There should be more lines at the sharply curved and pointed surfaces of the objects and less lines at the flatter sections.