Science in general and Physics in particular are concerned with relationships. Cause and effect is the focus of science. Nature is probed in order to find relationships and mathematical patterns. Scientists modify a set of conditions to see if there is a pattern of behavior in another set of measurable quantities. The goal is to answer the question of how does a change in a set of variables or conditions causally affect an observable outcome? In Physics, this search for cause and effect leads to questions like:
How does a force affect the acceleration of an object?
How does the mass of an object affect its acceleration?
How does the speed of a falling object affect the amount of air resistance that it experiences?
How does the distance from a page to a light bulb affect the amount of light that illuminates the paper’s surface?
How does the frequency of a sound wave affect the speed at which the sound wave moves?
How does the distance between two charged objects affect the force of attraction or repulsion that they encounter?
This search for cause and effect often leads to conclusive evidence that two variables are causally related (or not causally related). Careful observation and measurement might indicate that a pattern exists in which an increase in one variable always causes another measurable quantity to increase. This type of cause-effect relationship is described as being a direct relationship. Observation might also indicate that an increase in one variable always causes another measurable quantity to decrease. This type of cause-effect relationship is described as being an inverse relationship.
Inverse relationships are common in nature. In electrostatics, the electrical force between two charged objects is inversely related to the distance of separation between the two objects. Increasing the separation distance between objects decreases the force of attraction or repulsion between the objects. And decreasing the separation distance between objects increases the force of attraction or repulsion between the objects. Electrical forces are extremely sensitive to distance. These observations are commonly made during demonstrations and lab experiments. Consider a charged plastic golf tube being brought near a collection of paper bits at rest upon a table. The electrical interaction is so small at large distances that the golf tube does not seem to exert an influence upon the paper bits. Yet if the tube is brought closer, an attractive interaction is observed and the strength is so significant that the paper bits are lifted off the table. In a similar manner, charged balloons are observed to exert their greatest influence upon other charged objects when the separation distance is reduced. Electrostatic force and distance are inversely related.
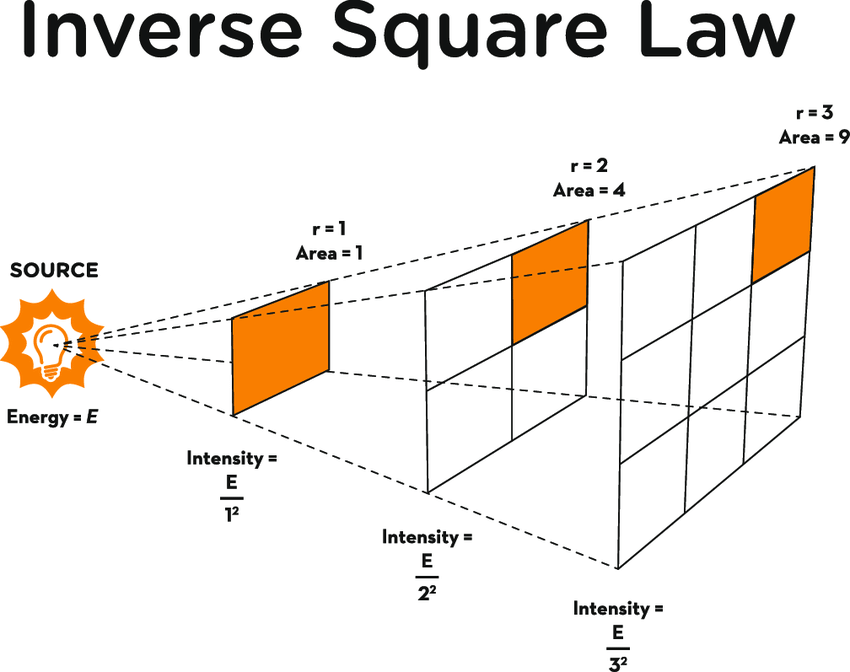
The pattern between electrostatic force and distance can be further characterized as an inverse square relationship. Careful observations show that the electrostatic force between two point charges varies inversely with the square of the distance of separation between the two charges. That is, the factor by which the electrostatic force is changed is the inverse of the square of the factor by which the separation distance is changed. So if the separation distance is doubled (increased by a factor of 2), then the electrostatic force is decreased by a factor of four (2 raised to the second power). And if the separation distance is tripled (increased by a factor of 3), then the electrostatic force is decreased by a factor of nine (3 raised to the second power). This square effect makes distance of double importance in its impact upon electrostatic force.
The inverse square relationship between electrostatic force and separation distance is illustrated in the table below.
| Row | Separation Distance | Electrostatic Force |
| 1 | 20.0 cm | 0.1280 N |
| 2 | 40.0 cm | 0.0320 N |
| 3 | 60.0 cm | 0.0142 N |
| 4 | 80.0 cm | 0.0080 N |
| 5 | 100.0 cm | 0.0051 N |
The above values illustrate a pattern: as the separation distance is doubled, the electrostatic force is decreased by a factor of four. For instance, the distance in Row 2 is twice the distance of Row 1; and the electrostatic force in Row 2 is one-fourth the electrostatic force of Row 1. A comparison of Row 1 and Row 3 illustrate that as the distance is increased by a factor three, the force is decreased by a factor of nine. The distance in Row 3 is three times that of Row 1 and the force in Row 3 is one-ninth that of Row 1. A similar comparison of Rows 1 and Row 4 illustrates that as the distance is increased by a factor of four, the electrostatic force is decreased by a factor of 16. The distance in Row 4 is four times that of Row 1 and the force in Row 4 is one-sixteenth that of Row 1.
The inverse square relationship between force and distance is expressed in the Coulomb’s law equation for electrostatic force. In the previous section of Lesson 3, Coulomb’s law was stated as
This equation is often used as a recipe for algebraic problem solving. This type of use of the Coulomb’s law equation was the subject of the previous section of Lesson 3. The equation shows that the distance squared term is in the denominator of the equation, opposite the force. This illustrates that force is inversely proportional to the square of the distance.
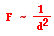
Understanding this inverse proportionality allows one to use the equation as a guide to thinking about how a variation in one quantity (e.g., distance) affects another quantity (Force). Equations can be more than merely recipes for algebraic problem solving; they can be “guides to thinking.” Check your understanding of Coulomb’s law as a guide to thinking by answering the questions below. When finished, click the button to check your answers.
Check Your Understanding
Use your understanding of charge to answer the following questions. When finished, click the button to view the answers.
Alteration in the Quantity of Charge
1. Two charged objects have a repulsive force of 0.080 N. If the charge of one of the objects is doubled, then what is the new force?
See Answer
Answer: 0.160 N
Explanation: Electrostatic force is directly related to the charge of each object. So if the charge of one object is doubled, then the force will become two times greater. Two times 0.080 N is 0.160 N.
2. Two charged objects have a repulsive force of 0.080 N. If the charge of both of the objects is doubled, then what is the new force?
See Answer
Answer: 0.320 N
Explanation: Electrostatic force is directly related to the charge of each object. So if the charge of both objects is doubled, then the force will become four times greater. Four times 0.080 N is 0.320 N.
Alteration in the Distance between Charged Objects
3. Two charged objects have a repulsive force of 0.080 N. If the distance separating the objects is doubled, then what is the new force?
See Answer
Answer: 0.020 N
Explanation: The electrostatic force is inversely related to the square of the separation distance. So if d is two times larger, then F is four times smaller – that is, one-fourth the original value. One-fourth of 0.080 N is 0.020 N.
4. Two charged objects have a repulsive force of 0.080 N. If the distance separating the objects is tripled, then what is the new force?
See Answer
Answer: 0.00889 N
Explanation: The electrostatic force is inversely related to the square of the separation distance. So if d is three times larger, then F is nine times smaller – that is, one-ninth the original value. One-ninth of 0.080 N is 0.00889 N.
close
5. Two charged objects have an attractive force of 0.080 N. If the distance separating the objects is quadrupled, then what is the new force?
See Answer
Answer: 0.0050 N
Explanation: The electrostatic force is inversely related to the square of the separation distance. So if d is four times larger (quadrupled), then F is 16 times smaller – that is, 1/16-th the original value. One-sixteenth of 0.080 N is 0.0050 N.
6. Two charged objects have a repulsive force of 0.080 N. If the distance separating the objects is halved, then what is the new force?
See Answer
Answer: 0.320 N
Explanation: The electrostatic force is inversely related to the square of the separation distance. So if d is two times smaller, then F is four times larger. Four times 0.080 N is 0.320 N
Alteration in both the Quantity of Charge and the Distance
7. Two charged objects have a repulsive force of 0.080 N. If the charge of one of the objects is doubled, and the distance separating the objects is doubled, then what is the new force?
See Answer
Answer: 0.040 N
Explanation: The electrostatic force is directly related to the product of the charges and inversely related to the square of the separation distance. Doubling one of the charges would serve to double the force. Doubling the distance would serve to reduce the force by a factor of four. The combined affect of these two variations would be to decrease the force by a factor of two – changing it from 0.080 N to 0.040 N
8. Two charged objects have a repulsive force of 0.080 N. If the charge of both of the objects is doubled and the distance separating the objects is doubled, then what is the new force?
See Answer
Answer: 0.080 N
Explanation: The electrostatic force is directly related to the product of the charges and inversely related to the square of the separation distance. Doubling both of the charges would serve to quadruple the force. Doubling the distance would serve to reduce the force by a factor of four. The combined affect of these two variations would be to not change the force at all; it remains as 0.080 N.
9. Two charged objects have an attractive force of 0.080 N. If the charge of one of the objects is increased by a factor of four, and the distance separating the objects is doubled, then what is the new force?
See Answer
Answer: 0.080 N
Explanation: The electrostatic force is directly related to the product of the charges and inversely related to the square of the separation distance. Quadrupling one of the charges would serve to quadruple the force. Doubling the distance would serve to reduce the force by a factor of four. The combined affect of these two variations would be to not alter the force at all; it would remain as 0.080 N.
10. Two charged objects have an attractive force of 0.080 N. If the charge of one of the objects is tripled and the distance separating the objects is tripled, then what is the new force?
See Answer
Answer: 0.0267 N
Explanation: The electrostatic force is directly related to the product of the charges and inversely related to the square of the separation distance. Tripling one of the charges would serve to triple the force. Tripling the distance would serve to reduce the force by a factor of nine. The combined affect of these two variations would be to make the force 3/9-ths or 1/3-rd the original value. One-third of 0.080 N is 0.0267 N.
