If you have been following along since the beginning of this lesson, then you have been developing a progressively sophisticated understanding of temperature and heat. You should be developing a model of matter as consisting of particles which vibrate (wiggle about a fixed position), translate (move from one location to another) and even rotate (revolve about an imaginary axis). These motions give the particles kinetic energy. Temperature is a measure of the average amount of kinetic energy possessed by the particles in a sample of matter. The more the particles vibrate, translate and rotate, the greater the temperature of the object. You have hopefully adopted an understanding of heat as a flow of energy from a higher temperature object to a lower temperature object. It is the temperature difference between the two neighboring objects that causes this heat transfer. The heat transfer continues until the two objects have reached thermal equilibrium and are at the same temperature. The discussion of heat transfer has been structured around some everyday examples such as the cooling of a hot mug of coffee and the warming of a cold can of pop. Finally, we have explored a thought experiment in which a metal can containing hot water is placed within a Styrofoam cup containing cold water. Heat is transferred from the hot water to the cold water until both samples have the same temperature.
 Now we should probe some of the following questions:
Now we should probe some of the following questions:
· What is happening at the particle level when energy is being transferred between two objects?
· Why is thermal equilibrium always established when two objects transfer heat?
· How does heat transfer work within the bulk of an object?
· Is there more than one method of heat transfer? If so, then how are they similar and different than one another?
Conduction – A Particle View
Let’s begin our discussion by returning to our thought experiment in which a metal can containing hot water was placed within a Styrofoam cup containing cold water. Heat is transferred from the hot water to the cold water until both samples have the same temperature. In this instance, the transfer of heat from the hot water through the metal can to the cold water is sometimes referred to as conduction. Conductive heat flow involves the transfer of heat from one location to another in the absence of any material flow. There is nothing physical or material moving from the hot water to the cold water. Only energy is transferred from the hot water to the cold water. Other than the loss of energy, there is nothing else escaping from the hot water. And other than the gain of energy, there is nothing else entering the cold water. How does this happen? What is the mechanism that makes conductive heat flow possible?
 A question like this is a particle-level question. To understand the answer, we have to think about matter as consisting of tiny particles atoms, molecules and ions. These particles are in constant motion; this gives them kinetic energy. As mentioned previously in this lesson, these particles move throughout the space of a container, colliding with each other and with the walls of their container. This is known as translational kinetic energy and is the main form of kinetic energy for gases and liquids. But these particles can also vibrate about a fixed position. This gives the particles vibrational kinetic energy and is the main form of kinetic energy for solids. To put it more simply, matter consists of little wigglers and little bangers. The wigglers are those particles vibrating about a fixed position. They possess vibrational kinetic energy. The bangers are those particles that move through the container with translational kinetic energy and collide with the container walls.
A question like this is a particle-level question. To understand the answer, we have to think about matter as consisting of tiny particles atoms, molecules and ions. These particles are in constant motion; this gives them kinetic energy. As mentioned previously in this lesson, these particles move throughout the space of a container, colliding with each other and with the walls of their container. This is known as translational kinetic energy and is the main form of kinetic energy for gases and liquids. But these particles can also vibrate about a fixed position. This gives the particles vibrational kinetic energy and is the main form of kinetic energy for solids. To put it more simply, matter consists of little wigglers and little bangers. The wigglers are those particles vibrating about a fixed position. They possess vibrational kinetic energy. The bangers are those particles that move through the container with translational kinetic energy and collide with the container walls.
The container walls represent the perimeters of a sample of matter. Just as the perimeter of your property(as in real estate property) is the furthest extension of the property, so the perimeter of an object is the furthest extension of the particles within a sample of matter. At the perimeter, the little bangers are colliding with particles of another substance – the particles of the container or even the surrounding air. Even the wigglers that are fixed in a position along the perimeter are doing some banging. Being at the perimeter, their wiggling results in collisions with the particles that are next to them; these are the particles of the container or of the surrounding air.
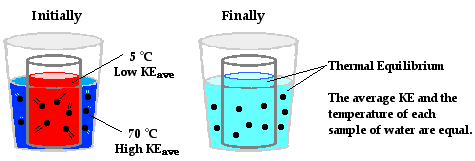
 At this perimeter or boundary, the collisions of the little bangers and wigglers are elastic collisions in which the total amount of kinetic energy of all colliding particles is conserved. The net effect of these elastic collisions is that there is a transfer of kinetic energy across the boundary to the particles on the opposite side. The more energetic particles will lose a little kinetic energy and the less energetic particles will gain a little kinetic energy. Temperature is a measure of the average amount of kinetic energy possessed by the particles in a sample of matter. So on average, there are more particles in the higher temperature object with greater kinetic energy than there are in the lower temperature object. So when we average all the collisions together and apply the principles associated with elastic collisions to the particles within a sample of matter, it is logical to conclude that the higher temperature object will lose some kinetic energy and the lower temperature object will gain some kinetic energy. The collisions of our little bangers and wigglers will continue to transfer energy until the temperatures of the two objects are identical. When this state of thermal equilibrium has been reached, the average kinetic energy of both objects’ particles is equal. At thermal equilibrium, there are an equal number of collisions resulting in an energy gain as there are collisions resulting in an energy loss. On average, there is no net energy transfer resulting from the collisions of particles at the perimeter.
At this perimeter or boundary, the collisions of the little bangers and wigglers are elastic collisions in which the total amount of kinetic energy of all colliding particles is conserved. The net effect of these elastic collisions is that there is a transfer of kinetic energy across the boundary to the particles on the opposite side. The more energetic particles will lose a little kinetic energy and the less energetic particles will gain a little kinetic energy. Temperature is a measure of the average amount of kinetic energy possessed by the particles in a sample of matter. So on average, there are more particles in the higher temperature object with greater kinetic energy than there are in the lower temperature object. So when we average all the collisions together and apply the principles associated with elastic collisions to the particles within a sample of matter, it is logical to conclude that the higher temperature object will lose some kinetic energy and the lower temperature object will gain some kinetic energy. The collisions of our little bangers and wigglers will continue to transfer energy until the temperatures of the two objects are identical. When this state of thermal equilibrium has been reached, the average kinetic energy of both objects’ particles is equal. At thermal equilibrium, there are an equal number of collisions resulting in an energy gain as there are collisions resulting in an energy loss. On average, there is no net energy transfer resulting from the collisions of particles at the perimeter.
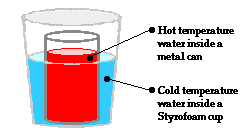 At the macroscopic level, heat is the transfer of energy from the high temperature object to the low temperature object. At the particle level, heat flow can be explained in terms of the net effect of the collisions of a whole bunch of little bangers. Warming and cooling is the macroscopic result of this particle-level phenomenon. Now let’s apply this particle view to the scenario of the metal can with the hot water positioned inside of a Styrofoam cup containing cold water. On average, the particles with the greatest kinetic energy are the particles of the hot water. Being a fluid, those particles move about with translational kinetic energy and bang uponthe particles of the metal can. As the hot water particles bang upon the particles of the metal can, they transfer energy to the metal can. This warms the metal can up. Most metals are good thermal conductors so they warm up quite quickly throughout the bulk of the can. The can assumes nearly the same temperature as the hot water. Being a solid, the metal can consists of little wigglers. The wigglers at the outer perimeter of the metal can bang upon particles in the cold water. The collisions between the particles of the metal can and the particles of the cold water result in the transfer of energy to the cold water. This slowly warms the cold water up. The interaction between the particles of the hot water, the metal can and the cold water results in a transfer of energy outward from the hot water to the cold water. The average kinetic energy of the hot water particles gradually decreases; the average kinetic energy of the cold-water particles gradually increases; and eventually, thermal equilibrium would be reached at the point that the particles of the hot water and the cold water have the same average kinetic energy. At the macroscopic level, one would observe a decrease in temperature of the hot water and an increase in temperature of the cold water.
At the macroscopic level, heat is the transfer of energy from the high temperature object to the low temperature object. At the particle level, heat flow can be explained in terms of the net effect of the collisions of a whole bunch of little bangers. Warming and cooling is the macroscopic result of this particle-level phenomenon. Now let’s apply this particle view to the scenario of the metal can with the hot water positioned inside of a Styrofoam cup containing cold water. On average, the particles with the greatest kinetic energy are the particles of the hot water. Being a fluid, those particles move about with translational kinetic energy and bang uponthe particles of the metal can. As the hot water particles bang upon the particles of the metal can, they transfer energy to the metal can. This warms the metal can up. Most metals are good thermal conductors so they warm up quite quickly throughout the bulk of the can. The can assumes nearly the same temperature as the hot water. Being a solid, the metal can consists of little wigglers. The wigglers at the outer perimeter of the metal can bang upon particles in the cold water. The collisions between the particles of the metal can and the particles of the cold water result in the transfer of energy to the cold water. This slowly warms the cold water up. The interaction between the particles of the hot water, the metal can and the cold water results in a transfer of energy outward from the hot water to the cold water. The average kinetic energy of the hot water particles gradually decreases; the average kinetic energy of the cold-water particles gradually increases; and eventually, thermal equilibrium would be reached at the point that the particles of the hot water and the cold water have the same average kinetic energy. At the macroscopic level, one would observe a decrease in temperature of the hot water and an increase in temperature of the cold water.
The mechanism in which heat is transferred from one object to another object through particle collisions is known as conduction. In conduction, there is no net transfer of physical stuff between the objects. Nothing material moves across the boundary. The changes in temperature are wholly explained as the result of the gains and losses of kinetic energy during collisions.
Conduction Through The Bulk of an Object
We have discussed how heat transfers from one object to another through conduction. But how does it transfer through the bulk of an object? For instance, suppose we pull a ceramic coffee mug out of the cupboard and place it on the countertop. The mug is at room temperature – maybe at 26°C. Then suppose we fill the ceramic coffee mug with hot coffee at a temperature of 80°C. The mug quickly warms up. Energy first flows into the particles at the boundary between the hot coffee and the ceramic mug. But then it flows through the bulk of the ceramic to all parts of the ceramic mug. How does heat conduction occur in the ceramic itself?
The mechanism of heat transfer through the bulk of the ceramic mug is described in a similar manner as it before. The ceramic mug consists of a collection of orderly arranged wigglers. These are particles that wiggle about a fixed position. As the ceramic particles at the boundary between the hot coffee and the mug warm up, they attain a kinetic energy that is much higher than their neighbors. As they wiggle more vigorously, they bang into their neighbors and increase their vibrational kinetic energy. These particles in turn begin to wiggle more vigorously and their collisions with their neighbors increase their vibrational kinetic energy. The process of energy transfer by means of the littlebangers continues from the particles at the inside of the mug (in contact with the coffee particles) to the outside of the mug (in contact with the surrounding air). Soon the entire coffee mug is warm and your hand feels it.
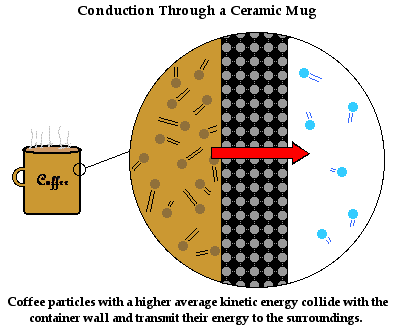
This mechanism of conduction by particle-to-particle interaction is very common in ceramic materials such as a coffee mug. Does it work the same in metal objects? For instance, you likely have noticed the high temperatures attained by the metal handle of a skillet when placed upon a stovetop. The burners on the stove transfer heat to the metal skillet. If the handle of the skillet is metallic, it too attains a high temperature, certainly high enough to cause a bad burn. The transfer of heat from the skillet to the skillet handle occurs by conduction. But in metals, the conduction mechanism is slightly more complicated. In a manner similar to electrical conductivity, thermal conductivity in metals occurs by the movement of free electrons. Outer shell electrons of metal atoms are shared among atoms and are free to move throughout the bulk of the metal. These electrons carry the energy from the skillet to the skillet handle. The details of this mechanism of thermal conduction in metals are considerably more complex than the discussion given here. The main point to grasp is that heat transfer through metals occurs without any movement of atoms from the skillet to the skillet handle. This qualifies the heat transfer as being categorized as thermal conduction.
Heat Transfer by Convection
 Is conduction the only means of heat transfer? Can heat be transferred through the bulk of an object in methods other than conduction? The answer is yes. The model of heat transfer through the ceramic coffee mug and the metal skillet involved conduction. The ceramic of the coffee mug and the metal of the skillet are both solids. Heat transfer through solids occurs by conduction. This is primarily due to the fact that solids have orderly arrangements of particles that are fixed in place. Liquids and gases are not very good conductors of heat. In fact, they are considered good thermal insulators. Heat typically does not flow through liquids and gases by means of conduction. Liquids and gases are fluids; their particles are not fixed in place; they move about the bulk of the sample of matter. The model used for explaining heat transfer through the bulk of liquids and gases involves convection. Convection is the process of heat transfer from one location to the next by the movement of fluids. The moving fluid carries energy with it. The fluid flows from a high temperature location to a low temperature location.
Is conduction the only means of heat transfer? Can heat be transferred through the bulk of an object in methods other than conduction? The answer is yes. The model of heat transfer through the ceramic coffee mug and the metal skillet involved conduction. The ceramic of the coffee mug and the metal of the skillet are both solids. Heat transfer through solids occurs by conduction. This is primarily due to the fact that solids have orderly arrangements of particles that are fixed in place. Liquids and gases are not very good conductors of heat. In fact, they are considered good thermal insulators. Heat typically does not flow through liquids and gases by means of conduction. Liquids and gases are fluids; their particles are not fixed in place; they move about the bulk of the sample of matter. The model used for explaining heat transfer through the bulk of liquids and gases involves convection. Convection is the process of heat transfer from one location to the next by the movement of fluids. The moving fluid carries energy with it. The fluid flows from a high temperature location to a low temperature location.
 To understand convection in fluids, let’s consider the heat transfer through the water that is being heated in a pot on a stove. Of course the source of the heat is the stove burner. The metal pot that holds the water is heated by the stove burner. As the metal becomes hot, it begins to conduct heat to the water. The water at the boundary with the metal pan becomes hot. Fluids expand when heated and become less dense. So as the water at the bottom of the pot becomes hot, its density decreases. Differences in water density between the bottom of the pot and the top of the pot results in the gradual formation of circulation currents. Hot water begins to rise to the top of the pot displacing the colder water that was originally there. And the colder water that was present at the top of the pot moves towards the bottom of the pot where it is heated and begins to rise. These circulation currents slowly develop over time, providing the pathway for heated water to transfer energy from the bottom of the pot to the surface.
To understand convection in fluids, let’s consider the heat transfer through the water that is being heated in a pot on a stove. Of course the source of the heat is the stove burner. The metal pot that holds the water is heated by the stove burner. As the metal becomes hot, it begins to conduct heat to the water. The water at the boundary with the metal pan becomes hot. Fluids expand when heated and become less dense. So as the water at the bottom of the pot becomes hot, its density decreases. Differences in water density between the bottom of the pot and the top of the pot results in the gradual formation of circulation currents. Hot water begins to rise to the top of the pot displacing the colder water that was originally there. And the colder water that was present at the top of the pot moves towards the bottom of the pot where it is heated and begins to rise. These circulation currents slowly develop over time, providing the pathway for heated water to transfer energy from the bottom of the pot to the surface.
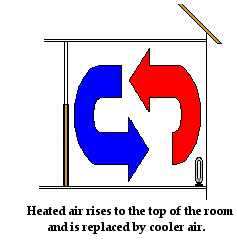 Convection also explains how an electric heater placed on the floor of a cold room warms up the air in the room. Air present near the coils of the heater warm up. As the air warms up, it expands, becomes less dense and begins to rise. As the hot air rises, it pushes some of the cold air near the top of the room out of the way. The cold air moves towards the bottom of the room to replace the hot air that has risen. As the colder air approaches the heater at the bottom of the room, it becomes warmed by the heater and begins to rise. Once more, convection currents are slowly formed. Air travels along these pathways, carrying energy with it from the heater throughout the room.
Convection also explains how an electric heater placed on the floor of a cold room warms up the air in the room. Air present near the coils of the heater warm up. As the air warms up, it expands, becomes less dense and begins to rise. As the hot air rises, it pushes some of the cold air near the top of the room out of the way. The cold air moves towards the bottom of the room to replace the hot air that has risen. As the colder air approaches the heater at the bottom of the room, it becomes warmed by the heater and begins to rise. Once more, convection currents are slowly formed. Air travels along these pathways, carrying energy with it from the heater throughout the room.
Convection is the main method of heat transfer in fluids such as water and air. It is often said that heat rises in these situations. The more appropriate explanation is to say that heated fluid rises. For instance, as the heated air rises from the heater on a floor, it carries more energetic particles with it. As the more energetic particles of the heated air mix with the cooler air near the ceiling, the average kinetic energy of the air near the top of the room increases. This increase in the average kinetic energy corresponds to an increase in temperature. The net result of the rising hot fluid is the transfer of heat from one location to another location. The convection method of heat transfer always involves the transfer of heat by the movement of matter. This is not to be confused with the caloric theory discussed earlier in this lesson. In caloric theory, heat was the fluid and the fluid that moved was the heat. Our model of convection considers heat to be energy transfer that is simply the result of the movement of more energetic particles.
The two examples of convection discussed here – heating water in a pot and heating air in a room – are examples of natural convection. The driving force of the circulation of fluid is natural – differences in density between two locations as the result of fluid being heated at some source. (Some sources introduce the concept of buoyant forces to explain why the heated fluids rise. We will not pursue such explanations here.) Natural convection is common in nature. The earth’s oceans and atmosphere are heated by natural convection. In contrast to natural convection, forced convection involves fluid being forced from one location to another by fans, pumps and other devices. Many home heating systems involve force air heating. Air is heated at a furnace and blown by fans through ductwork and released into rooms at vent locations. This is an example of forced convection. The movement of the fluid from the hot location (near the furnace) to the cool location (the rooms throughout the house) is driven or forced by a fan. Some ovens are forced convection ovens; they have fans that blow heated air from a heat source into the oven. Some fireplaces enhance the heating ability of the fire by blowing heated air from the fireplace unit into the adjacent room. This is another example of forced convection.
Heat Transfer by Radiation
A final method of heat transfer involves radiation. Radiation is the transfer of heat by means ofelectromagnetic waves. To radiate means to send out or spread from a central location. Whether it is light, sound, waves, rays, flower petals, wheel spokes or pain, if something radiates then it protrudes or spreads outward from an origin. The transfer of heat by radiation involves the carrying of energy from an origin to the space surrounding it. The energy is carried by electromagnetic waves and does not involve the movement or the interaction of matter. Thermal radiation can occur through matter or through a region of space that is void of matter (i.e., a vacuum). In fact, the heat received on Earth from the sun is the result of electromagnetic waves traveling through the void of space between the Earth and the sun.
All objects radiate energy in the form of electromagnetic waves. The rate at which this energy is released is proportional to the Kelvin temperature (T) raised to the fourth power.
Radiation rate = k•T4
The hotter the object, the more it radiates. The sun obviously radiates off more energy than a hot mug of coffee. The temperature also affects the wavelength and frequency of the radiated waves. Objects at typical room temperatures radiate energy as infrared waves. Being invisible to the human eye, we do not see this form of radiation. An infrared camera is capable of detecting such radiation. Perhaps you have seen thermal photographs or videos of the radiation surrounding a person or animal or a hot mug of coffee or the Earth. The energy radiated from an object is usually a collection or range of wavelengths. This is usually referred to as an emission spectrum. As the temperature of an object increases, the wavelengths within the spectra of the emitted radiation also decrease. Hotter objects tend to emit shorter wavelength, higher frequency radiation. The coils of an electric toaster are considerably hotter than room temperature and emit electromagnetic radiation in the visible spectrum. Fortunately, this provides a convenient warning to its users that the coils are hot. The tungsten filament of an incandescent light bulb emits electromagnetic radiation in the visible (and beyond) range. This radiation not only allows us to see, it also warms the glass bulb that contains the filament. Put your hand near the bulb (without touching it) and you will feel the radiation from the bulb as well.
Thermal radiation is a form of heat transfer because the electromagnetic radiation emitted from the source carries energy away from the source to surrounding (or distant) objects. This energy is absorbed by those objects, causing the average kinetic energy of their particles to increase and causing the temperatures to rise. In this sense, energy is transferred from one location to another by means of electromagnetic radiation. The image at the right was taken by a thermal imaging camera. The camera detects the radiation emitted by objects and represents it by means of a color photograph. The hotter colors represent areas of objects that are emitting thermal radiation at a more intense rate. (Images courtesy Peter Lewis and Chris West of Standford’s SLAC.)
Our discussion on this page has pertained to the various methods of heat transfer. Conduction, convection and radiation have been described and illustrated. The macroscopic has been explained in terms of the particulate – an ongoing goal of this chapter of The Physics Classroom Tutorial. The last topic to be discussed in Lesson 1 is more quantitative in nature. On the next page, we will investigate the mathematics associated with the rate of heat transfer.
Check Your Understanding
1. Consider Object A which has a temperature of 65°C and Object B which has a temperature of 15°C. The two objects are placed next to each other and the little bangers begin colliding. Will any of the collisions result in the transfer of energy from Object B to Object A? Explain.
See Answer

Answer: Most certainly yes.
The average kinetic energy of the particles in Object A is greater than the average kinetic energy of the particles in Object B. But there is a range of speeds and thus of kinetic energy in both objects. As such, there will be some highly energetic particles in Object B and some very non-energetic particles in Object A. When this combination of particles encounter a collision, there will a transfer of energy across the boundary from Object B (the colder object) to Object A (the hotter object). This is just one collision. Since majority of collisions result from the more energetic particles of Object A with less energetic particles of collision B, there will be a net kinetic energy transfer from Object A to Object B.
2. Suppose that Object A and Object B (from the previous problem) have reached a thermal equilibrium. Do the particles of the two objects still collide with each other? If so, do any of the collisions result in the transfer of energy between the two objects? Explain.
See Answer

Answer:
The collisions will still take place because the particles are still moving. Just because the temperatures are the same doesn’t mean the collisions will stop. The fact that the temperature is identical means that the average kinetic energy of all the particles is the same for both objects. As such, there will be just as much energy transferred from Object B to Object A as there is energy transferred in the opposite direction. When the effect of these collisions is averaged, there is no net energy transfer. This explains why the temperature of the two objects remains the same. Thermal equilibrium persists.


