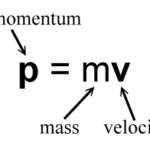
Since total system momentum is conserved in an explosion occurring in an isolated system, momentum principles can be used to make predictions about the resulting velocity of an object. Problem solving for explosion situations is a common part of most high school physics experiences. Consider for instance the following problem:
A 56.2-gram tennis ball is loaded into a 1.27-kg homemade cannon. The cannon is at rest when it is ignited. Immediately after the impulse of the explosion, a photogate timer measures the cannon to recoil backwards a distance of 6.1 cm in 0.0218 seconds. Determine the post-explosion speed of the cannon and of the tennis ball.
Like any problem in physics, this one is best approached by listing the known information.
Given:
| Cannon: | m = 1.27 kg | d = 6.1 cm | t = 0.0218 s |
| Ball: | m = 56.2 g = 0.0562 kg |
The strategy for solving for the speed of the cannon is to recognize that the cannon travels 6.1 cm at a constant speed in the 0.0218 seconds. The speed can be assumed constant since the problem states that it was measured after the impulse of the explosion when the acceleration had ceased. Since the cannon was moving at constant speed during this time, the distance/time ratio will provide a post-explosion speed value.
vcannon = d / t = (6.1 cm) / (0.0218 s) = 280 cm/s (rounded)
The strategy for solving for the post-explosion speed of the tennis ball involves using momentum conservation principles. If momentum is to be conserved, then the after-explosion momentum of the system must be zero (since the pre-explosion momentum was zero). For this to be true, then the post-explosion momentum of the tennis ball must be equal in magnitude (and opposite in direction) of that of the cannon. That is,
mball • vball = – mcannon • vcannon
The negative sign in the above equation serves the purpose of making the momenta of the two objects opposite in direction. Now values of mass and velocity can be substituted into the above equation to determine the post-explosion velocity of the tennis ball. (Note that a negative velocity has been inserted for the cannon’s velocity.)
(0.0562 kg) • vball = – (1.27 kg) • (-280 cm/s)
vball = – (1.27 kg) • (-280 cm/s) / (0.0562 kg)
vball = 6323.26 cm/s
vball = 63.2 m/s
Using momentum explosion, the ball is propelled forward with a speed of 63.2 m/s – that’s 141 miles/hour!
It’s worth noting that another method of solving for the ball’s velocity would be to use a momentum table similar to the one used previously in Lesson 2 for collision problems. In the table, the pre- and post-explosion momentum of the cannon and the tennis ball. This is illustrated below.
| Momentum Before Explosion | Momentum After Explosion | |
| Cannon | 0 | (1.27 kg) • (-280 cm/s)= -355 kg•cm/s |
| Tennis Ball | 0 | (0.0562 kg) • v |
| Total | 0 | 0 |
The variable v is used for the post-explosion velocity of the tennis ball. Using the table, one would state that the sum of the cannon and the tennis ball’s momentum after the explosion must sum to the total system momentum of 0 as listed in the last row of the table. Thus,
-355 kg•cm/s + (0.0562 kg) • v = 0
Solving for v yields 6323 cm/s or 63.2 m/s – consistent with the previous solution method.
Using the table means that you can use the same problem solving strategy for both collisions and explosions. After all, it is the same momentum conservation principle that governs both situations. Whether it is a collision or an explosion, if it occurs in an isolated system, then each object involved encounters the same impulse to cause the same momentum change. The impulse and momentum change on each object are equal in magnitude and opposite in direction. Thus, the total system momentum is conserved.
Check Your Understanding
1. Two pop cans are at rest on a stand. A firecracker is placed between the cans and lit. The firecracker explodes and exerts equal and opposite forces on the two cans. Assuming the system of two cans to be isolated, the post-explosion momentum of the system ____.
a. is dependent upon the mass and velocities of the two cans
b. is dependent upon the velocities of the two cans (but not their mass)
c. is typically a very large value
d. can be a positive, negative or zero value
e. is definitely zero
See Answer

Answer: E
Before the explosion, the cans were at rest. Thus, the pre-explosion momentum of the system was 0. If the system can be considered isolated (as stated), then the post-explosion momentum must also be 0.
2. Students of varying mass are placed on large carts and deliver impulses to each other’s carts, thus changing their momenta. In some cases, the carts are loaded with equal mass; in other cases they are unequal. In some cases, the students push off each other; in other cases, only one team does the pushing. For each situation, list the letter of the team that ends up with the greatest momentum. If they have the same momentum, then do not list a letter for that situation. Enter the four letters (or three or two or …) in alphabetical order.
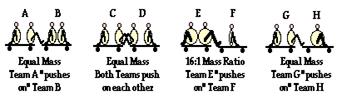
See Answer

Answer: — (don’t list any letters)
Don’t be fooled!! In each of the four situations, the two carts involved in the impulse encounter the same impulse causing the same momentum change which results in the same final momentum. Differences in mass will only effect the resulting velocity change. And if Team A “pushes on” Team B’s cart, then there is an equal and opposite reaction force exerted by Team B’s cart upon the legs of the Team A “pusher”. So there is never any situation in the given four in which one of the teams encounters a greater momentum.
3. Two ice dancers are at rest on the ice, facing each other with their hands together. They push off on each other in order to set each other in motion. The subsequent momentum change (magnitude only) of the two skaters will be ____.
a. greatest for the skater who is pushed upon with the greatest force
b. greatest for the skater who pushes with the greatest force
c. the same for each skater
d. greatest for the skater with the most mass
e. greatest for the skater with the least mass
See Answer

Answer: C
In this situation, the force on the first ice dancer is the same as the force on the second ice dancer (Newton’s third law of motion). And these forces act for the same amount of time to cause equal impulses on each skater. Since impulse is equal to momentum change, both skaters must also have equal momentum changes. The mass of the individual skaters will only effect the subsequent velocity change.
4. A 62.1-kg male ice skater is facing a 42.8-kg female ice skater. They are at rest on the ice. They push off each other and move in opposite directions. The female skater moves backwards with a speed of 3.11 m/s. Determine the post-impulse speed of the male skater.
See Answer

Answer: 2.14 m/s
| MomentumBefore Explosion | MomentumAfter Explosion | |
| Male Skater | 0 | (62.1 kg) • v |
| Female Skater | 0 | (42.8 kg) • (-3.11 m/s)= -133.11 kg•m/s |
| Total | 0 | 0 |
(62.1 kg) • v + (-133.11 kg•m/s) = 0
v = (133.11 kg•m/s) / (62.1 kg)
v = 2.14 m/s
5. A 1.5-kg cannon is mounted on top of a 2.0-kg cart and loaded with a 52.7-gram ball. The cannon, cart, and ball are moving forward with a speed of 1.27 m/s. The cannon is ignited and launches a 52.7-gram ball forward with a speed of 75 m/s. Determine the post-explosion velocity of the cannon and cart.
See Answer

Answer: 0.160 m/s (rounded)
| MomentumBefore Explosion | MomentumAfter Explosion | |
| Cart & Cannon | (3.5 kg) • (1.27 m/s)= 4.445 kg•m/s | (3.5 kg) • v |
| Tennis Ball | (0.0527 kg) • (1.27 m/s)= 0.06693 kg•m/s | (0.0527 kg) • (75 m/s)= 3.9525 kg•m/s |
| Total | 4.5119 kg•m/s | 4.5119 kg•m/s |
4.445 kg•m/s + 0.06693 kg•m/s = (3.5 kg) • v + 3.9525 kg•m/s
4.445 kg•m/s + 0.06693 kg•m/s – 3.9525 kg•m/s = (3.5 kg) • v
0.5594 kg •m/s = (3.5 kg) • v
(0.5594 kg •m/s) / (3.5 kg) = v
0.1598 m/s = v