The transformation of motion from one shaft to another shaft requires three bodies: a frame (the position of each shaft is fixed in the frame) and two gears. Consider a general case when two disks with arbitrary profiles shown in figure 1, represent gears 2 and 3. Also assume that disk 2 rotates with the constant angular velocity ω₂. The motion is transferred through the direct contact at point P (note that P₂ and P₃ are the same point P, but the first point is associated with disk 2 whereas the second point is associated with disk 3). We need to find out whether or not the angular velocity ω₃ will remain constant and if not, what is required to make it remain constant. The answer is given byKennedy’s theorem.

Kennedy’s theorem identifies the fundamental property of three rigid bodies in motion.

The three instantaneous centers shared by three rigid bodies in relative motion to one another all lie on the same straight line.

First, recall about that the instantaneous center of velocity, it is defined as the instantaneous location of a pair of coincident points of two different rigid bodies for which the absolute velocities of two points are equal. If one considers body 2 and the frame (represented by point O₂) in figure 1, then the instantaneous center of these two bodies is point O₂, which belongs to the frame and to disk 2. The absolute velocities of both bodies at point O₂ are zero.

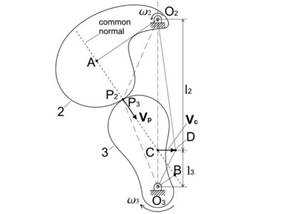
Figure 1: Kennedy’s theorem illustration

The same is valid for disk 3 and the frame represented by point O₃. For the three bodies in motion there are three instantaneous centers: for all combinations of pairs. Thus, there is an instantaneous center between the two disks.

Since point P is a common point for two disks in figure 1, for each disk the velocity component at this point directed along the common normal is the same and equal to V_p. One can move this velocity vector along the common normal until it intersects the line connecting the two instantaneous centers O₂ and O₃ at point C. According to Kennedy’s theorem, this point (P) is the instantaneous center of velocity for the two disks. Indeed, the velocity V_p, the only instantaneous common velocity for the two disks (disk 2, disk 3) will be equal to

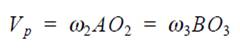
Triangles AO₂C and BO₃C are similar, it follows that

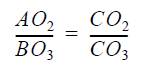
From the above relationship, the ratio of angular velocities is equal to

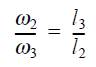
Where lengths l₂ and l₃ denote O₂C and O₃C, respectively (see the above figure 1).

Velocity V_c in figure 1 is a common velocity for the two disks since

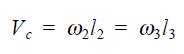
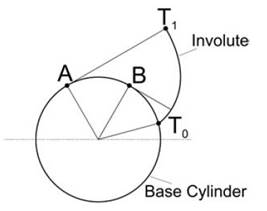
Figure 2: Illustration of the involute profile generation

Velocity V_c is also the absolute velocity of each body at this point because there cannot be another velocity component along the line O₂O₃ (since the distance between the frame points O₂ and O₃ is not changing and bodies 2 and 3 are assumed to be rigid).

Note that the relative velocity of two disks at point C is zero, whereas relative velocity at point P is not zero.

The above equation 3 gives the transformation of angular velocities from disk 2 to disk 3. It can be seen from the above relation, in order to remain kinematic ratio (ω₂/ω₃) constant, legthss l₂ and l₃ must not change. It is clear from figure 1, however, that for arbitrary profile shapes the common normal changes its direction during the motion, and thus point C moves along line O₂O₃. Thus, the problem of meeting the constant ratio requirement is to find such disk profiles that the kinematic ratio remains constant. It will be shown in the following that if the disk profile is described by theinvolute function, the common normal does not change its direction.