From the definition of momentum, it becomes obvious that an object has a large momentum if both its mass and its velocity are large. Both variables are of equal importance in determining the momentum of an object. Consider a Mack truck and a roller skate moving down the street at the same speed. The considerably greater mass of the Mack truck gives it a considerably greater momentum. Yet if the Mack truck were at rest, then the momentum of the least massive roller skate would be the greatest. The momentum of any object that is at rest is 0. Objects at rest do not have momentum – they do not have any “mass in motion.” Both variables – mass and velocity – are important in comparing the momentum of two objects.
The momentum equation can help us to think about how a change in one of the two variables might affect the momentum of an object. Consider a 0.5-kg physics cart loaded with one 0.5-kg brick and moving with a speed of 2.0 m/s. The total mass of loaded cart is 1.0 kg and its momentum is 2.0 kg•m/s. If the cart was instead loaded with three 0.5-kg bricks, then the total mass of the loaded cart would be 2.0 kg and its momentum would be 4.0 kg•m/s. A doubling of the mass results in a doubling of the momentum.
Similarly, if the 2.0-kg cart had a velocity of 8.0 m/s (instead of 2.0 m/s), then the cart would have a momentum of 16.0 kg•m/s (instead of 4.0 kg•m/s). Aquadrupling in velocity results in a quadrupling of the momentum. These two examples illustrate how the equation p = m•v serves as a “guide to thinking” andnot merely a “plug-and-chug recipe for algebraic problem-solving.”
Check Your Understanding
Express your understanding of the concept and mathematics of momentum by answering the following questions. Click the button to view the answers.
1. Determine the momentum of a …
a. 60-kg halfback moving eastward at 9 m/s.
b. 1000-kg car moving northward at 20 m/s.
c. 40-kg freshman moving southward at 2 m/s.
See Answer
A. p = m*v = 60 kg*9 m/s
p = 540 kg•m/s, east
B. p = m*v = 1000 kg*20 m/s
p = 20 000 kg•m/s, north
C. p = m*v = 40 kg*2 m/s
p = 80 kg•m/s, south
2. A car possesses 20 000 units of momentum. What would be the car’s new momentum if …
a. its velocity was doubled.
b. its velocity was tripled.
c. its mass was doubled (by adding more passengers and a greater load)
d. both its velocity was doubled and its mass was doubled.
See Answer
A. p = 40 000 units (doubling the velocity will double the momentum)
B. p = 60 000 units (tripling the velocity will triple the momentum)
C. p = 40 000 units (doubling the mass will double the momentum)
D. p = 80 000 units (doubling the velocity will double the momentum and doubling the mass will also double the momentum; the combined result is that the momentum is doubled twice -quadrupled)
3. A halfback (m = 60 kg), a tight end (m = 90 kg), and a lineman (m = 120 kg) are running down the football field. Consider their ticker tape patterns below.
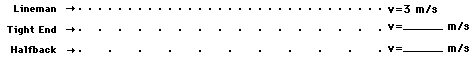
Compare the velocities of these three players. How many times greater are the velocity of the halfback and the velocity of the tight end than the velocity of the lineman?
Which player has the greatest momentum? Explain.
See Answer
A. The tight end travels twice the distance of the lineman in the same amount of time. Thus, the tight end is twice as fast (vtight end = 6 m/s). The halfback travels three times the distance of the lineman in the same amount of time. Thus, the halfback is three times as fast (vhalfback = 9 m/s).
B. Both the halfback and the tight end have the greatest momentum. The each have the same amount of momentum – 540 kg*m/s. The lineman only has 360 kg*m/s.
