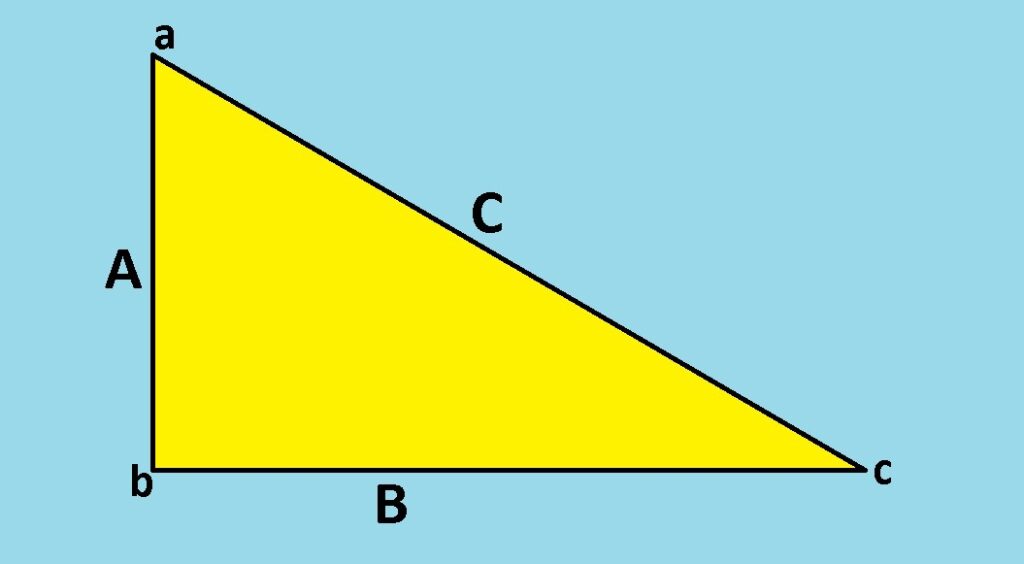
The Pythagorean theorem is a useful method for determining the result of adding two (and only two) vectors that make a right angle to each other. The method is not applicable for adding more than two vectors or for adding vectors that are not at 90-degrees to each other. The Pythagorean theorem is a mathematical equation that relates the length of the sides of a right triangle to the length of the hypotenuse of a right triangle.
To see how the method works, consider the following problem:
Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric’s resulting displacement.
This problem asks to determine the result of adding two displacement vectors that are at right angles to each other. The result (or resultant) of walking 11 km north and 11 km east is a vector directed northeast as shown in the diagram to the right. Since the northward displacement and the eastward displacement are at right angles to each other, the Pythagorean theorem can be used to determine the resultant (i.e., the hypotenuse of the right triangle).
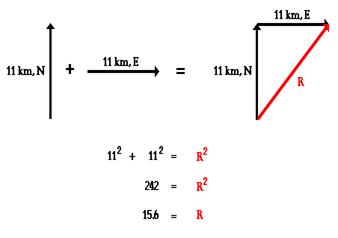
The result of adding 11 km, north plus 11 km, east is a vector with a magnitude of 15.6 km. Later, the method of determining the direction of the vector will be discussed.
Let’s test your understanding with the following two practice problems. In each case, use the Pythagorean theorem to determine the magnitude of the vector sum. When finished, click the button to view the answer.
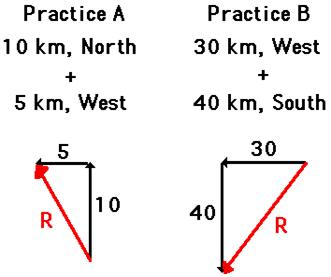
See Answer to Practice A
R2 = (5)2 + (10)2
R2 = 125
R = SQRT (125)
R = 11.2 km
See Answer to Practice B
R2 = (30)2 + (40)2
R2 = 2500
R = SQRT (2500)
R = 50 km
