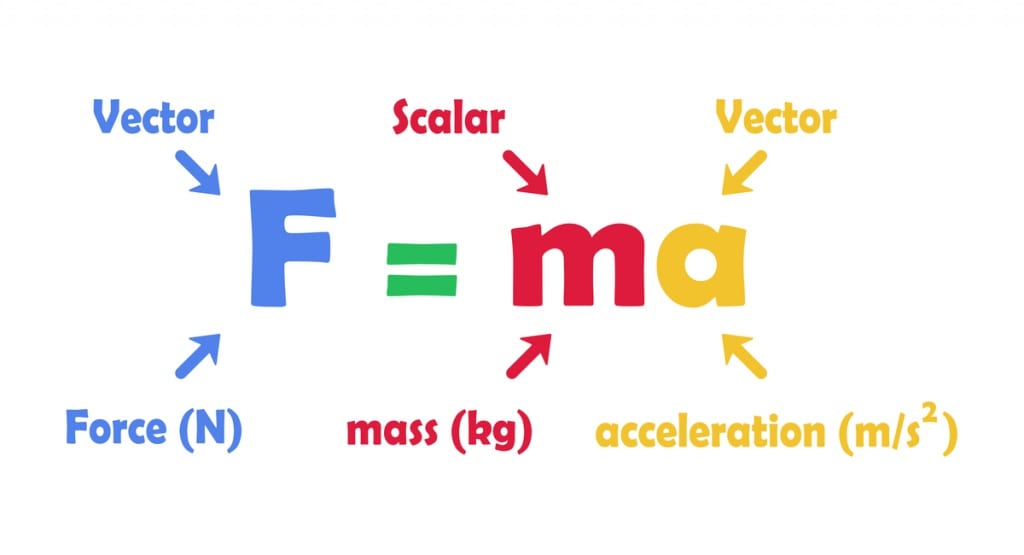
Newton’s second law of motion can be formally stated as follows:

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

This verbal statement can be expressed in equation form as follows:

a = F_net / m

The above equation is often rearranged to a more familiar form as shown below. The net force is equated to the product of the mass times the acceleration.

F_net = m • a

In this entire discussion, the emphasis has been on the net force. The acceleration is directly proportional to the net force; the net force equals mass times acceleration; the acceleration in the same direction as the net force; an acceleration is produced by a net force. The NET FORCE. It is important to remember this distinction. Do not use the value of merely “any ‘ole force” in the above equation. It is the net force that is related to acceleration. As discussed in an earlier lesson, the net force is the vector sum of all the forces. If all the individual forces acting upon an object are known, then the net force can be determined. If necessary, review this principle by returning to the practice questions in Lesson 2.

Consistent with the above equation, a unit of force is equal to a unit of mass times a unit of acceleration. By substituting standard metric units for force, mass, and acceleration into the above equation, the following unit equivalency can be written.

1 Newton = 1 kg • m/s²

The definition of the standard metric unit of force is stated by the above equation. One Newton is defined as the amount of force required to give a 1-kg mass an acceleration of 1 m/s/s.