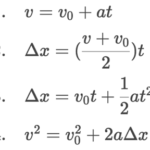The Kinematic Equations
The goal of this first unit of The Physics Classroom has been to investigate the variety of means by which the motion of objects can be described. The variety of representations that we have investigated includesverbal representations, pictorial representations, numerical representations, and graphical representations (position-time graphs and velocity-time graphs). In Lesson 6, we will investigate the use of equations to describe and represent the motion of objects. These equations are known as kinematic equations.
There are a variety of quantities associated with the motion of objects – displacement (and distance),velocity (and speed), acceleration, and time. Knowledge of each of these quantities provides descriptive information about an object’s motion. For example, if a car is known to move with a constant velocity of 22.0 m/s, North for 12.0 seconds for a northward displacement of 264 meters, then the motion of the car is fully described. And if a second car is known to accelerate from a rest position with an eastward acceleration of 3.0 m/s2 for a time of 8.0 seconds, providing a final velocity of 24 m/s, East and an eastward displacement of 96 meters, then the motion of this car is fully described. These two statements provide a complete description of the motion of an object. However, such completeness is not always known. It is often the case that only a few parameters of an object’s motion are known, while the rest are unknown. For example as you approach the stoplight, you might know that your car has a velocity of 22 m/s, East and is capable of a skidding acceleration of 8.0 m/s2, West. However you do not know the displacement that your car would experience if you were to slam on your brakes and skid to a stop; and you do not know the time required to skid to a stop. In such an instance as this, the unknown parameters can be determined using physics principles and mathematical equations (the kinematic equations).