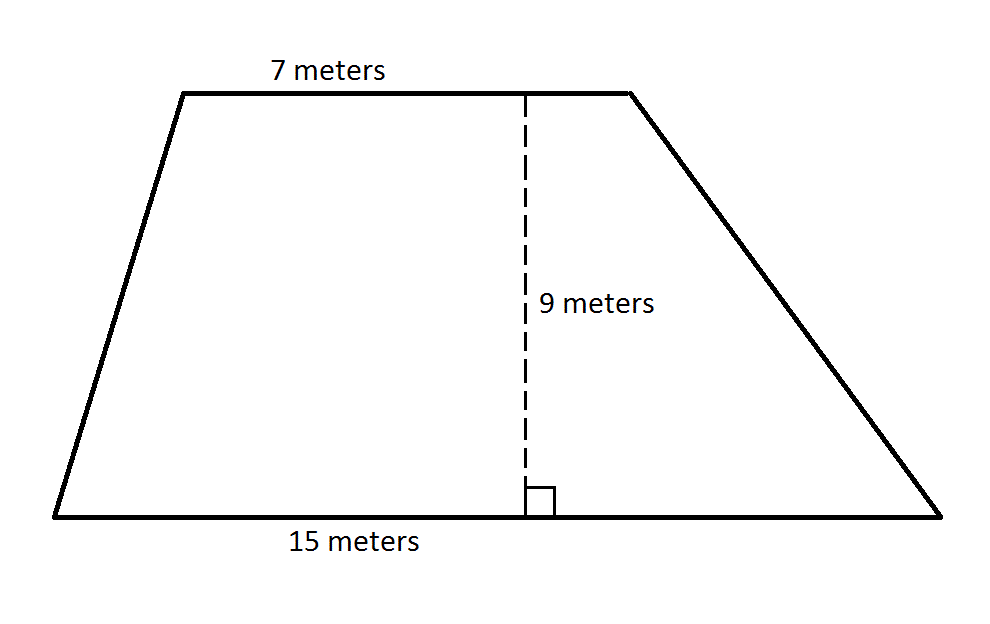
Finally we will look at a few example computations of the area for a few trapezoids. The solution for finding the area is shown for the first example below. The shaded trapezoid on the velocity-time graph has a base of 2 seconds and heights of 10 m/s (on the left side) and 30 m/s (on the right side). Since the area of trapezoid is found by using the formula A = ½ * (b) * (h1 + h2), the area is 40 m [½ * (2 s) * (10 m/s + 30 m/s)]. That is, the object was displaced 40 meters during the time interval from 1 second to 3 seconds.
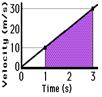 | Area = ½ * b * (h1 + h2) Area = ½ * (2 s) * (10 m/s + 30 m/s) Area = 40 m |
Now try the following two practice problems as a check of your understanding. Determine the displacement of the object during the time interval from 2 to 3 seconds (Practice A) and during the first 2 seconds (Practice B).


The area of a trapezoid is given by the formula
Area = ½ • b • (h1 + h2) where b = 1 s and h1 = 20 m/s and h2 = 30 m/s.
Area = ½ • (1 s) • (20 m/s + 30 m/s) = 25 m
That is, the object was displaced 25 m during the time interval from 2 to 3 wseconds.

The area of a trapezoid is given by the formula
Area = ½ • b • (h1 + h2) where b = 2 s and h1 = 30 m/s and h2 = 10 m/s
Area = ½ • (2 s) • (30 m/s + 10 m/s) = 40 m
That is, the object was displaced 40 m during the time interval from 2 to 3 seconds.