Sizing a hopper outlet or feed tube to achieve the required discharge rate is more difficult, but no less important, than overcoming arching, particularly for fine powders. All bulk materials have a maximum rate at which they discharge through a hopper opening of a given size (e.g., a Hall flowmeter test). For example, for free-flowing bulk materials, a good approximation of this maximum discharge rate of a coarse material (e.g., 3 mm and larger particles), from a mass flow hopper can be predicted:

where O is the maximum steady discharge rate, /is the bulk density, A is the cross-sectional area of outlet, B is the outlet diameter or width, g is the acceleration due to gravity, m is 1 for circular opening and 0 for slotted opening, and ^is the flow channel angle (measured from vertical) in degrees. This equation can be modified to take particle size into account, but this modification is only important if the particle size is a significant fraction of the outlet size (Ref 8).

Obviously most metal powders cannot be considered “coarse” materials; therefore, the above equation rarely applies in P/M applications.

For fine powders, funnel-flow bins often exhibit high discharge rates, but controlling the flow rate is always a challenge because the flow channel is not likely to be stable. As a result, the actual size and shape of the stagnant region is neither well defined nor constant. The flow channel can change size radically or collapse, creating flow rates that range from no-flow conditions to complete flooding.

Fine powders are more easily handled in a mass flow bin, whose flow channel is stable and predictable. Because all of the material is constantly moving in a mass flow bin, the flow channel is set by the shape of the bin.

However, it should be remembered that the maximum flow rate of a fine powder through the outlet of a mass flow bin is low compared with that of a coarse, granular solid. For fine materials, the expansion and contraction of voids during flow can create an upward air pressure gradient at the outlet of a mass flow bin. During discharge, this upward gradient acts against gravity, reducing the discharge rate. Such gradients do not usually form with coarser particle materials. Because coarse materials are more permeable than fine ones, air is allowed to flow freely into and out of the voids as they expand and contract.

This phenomenon can be analyzed by considering how gas flows through a bed of powder when a pressure differential occurs across the bed. When the gas velocity is low, flow through the bed is laminar, and Darcy’s law can be used to relate gas velocities to gas pressure gradients within or across the bed. Darcy’s law can be written in the following form:

where K is the permeability factor of the bulk solid, u is the superficial relative gas velocity through the bed of solids, 7 is the bulk density of the solid in the bed, and dp/dx is the gas pressure gradient acting at the point in the bed of solids where the velocity is being calculated. The permeability factor, K, has units of velocity and is inversely proportional to the viscosity of the gas. A permeability test is run by passing air (or other suitable gas) through a representative column of solids. The pressure across the bed is regulated, and the rate at which the gas flows is measured.

This approach allows the permeability of the bulk solid to be determined as a function of its bulk density. Figure 19 shows the test results for a sample of metal powder.

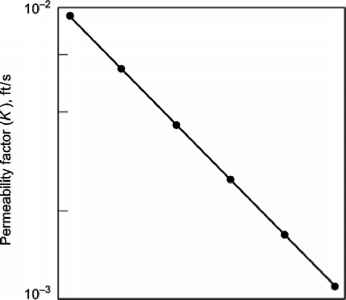
Fig. 19 Permeability as a function of bulk density (metal powder). Increases in bulk density reduce permeability of a material. Unless properly accounted for during bin selection, increased bulk density and reduced permeability can interrupt predictable flow.

Because mass flow bins have stable flow patterns that mimic the shape of the bin, permeability values can be used to calculate critical, steady-state discharge rates from mass flow hoppers. Permeability values can also be used to calculate the time required for fine powders to settle in bins and silos and to design solids processing vessels to purge, heat, dry, or condition bulk solids.