A final issue concerns the treatment of uncertainty. One method for explicitly introducing risk considerations is to treat benefits and costs as random variables which may be described by probability distributions. For exam-ple, an estimate of fire losses might consider the following events: no fire, minor fire, intermediate fire, and major fire. Each event has a probability of occurrence and an associ-ated damage loss. The total expected loss (EL) is given by
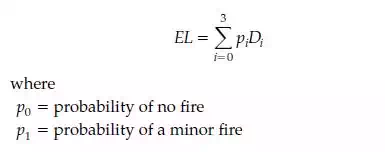
p2 =probability of an intermediate fire p3=probability of a major fire
Dn = associated damage loss, n =0,1,2,3
Expected losses may be computed for different fire protection strategies. Thus, a fire protection strategy that costs C3 and reduces damage losses of a major fire from D3 to D3 will result in an expected loss
EL = p0D0= p1D1= p2D2= p3D3= C3
Similarly, a fire control strategy that costs C2 and re-duces the probability of an intermediate fire from p2 to p2 has an expected loss
EL = p0D0= p1D1= p2D2= p3D3= C2
A comparison of expected losses from alternative strategies may then be used to determine the optimal strategy.
Use of expected value has a limitation in that only the average value of the probability distribution is consid-ered. Discussion of other procedures for evaluating un-certain outcomes is given by Anderson and Settle.6


