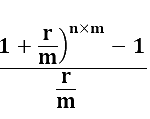Normally, but not always, the interest period is taken as 1 yr. There may be subperiods of quarters, months, weeks, and so forth.

Nominal versus effective interest: It is generally as-sumed that interest is compounded annually. However, interest may be compounded more frequently. When this occurs, there is a nominal interest or annual percentage rate and an effective interest, which is the figure used in calcu-lations. For example, a savings bank may offer 5 percent interest compounded quarterly, which is not the same as 5 percent per year. A nominal rate of 5 percent com-pounded quarterly is the same as 1.25 percent every three months or an effective rate of 5.1 percent per year. If

Continuous interest: A special case of effective interestoccurs when the number of periods per year is infinite. This represents a situation of continuous interest, also re-ferred to as continuous compounding. Formulas for con-tinuous interest can be derived by examining limits as M approaches infinity. Formulas for interest factors using continuous compounding are included in Appendix B. Continuous interest is compared to monthly interest in Table 5-7.1.

EXAMPLE:

Compare the future amounts obtained under various compounding periods at a nominal interest rate of 12 per-cent for 5 yr, if P = $10,000. (See Table 5-7.2.)

Series Payments

Life would be simpler if all financial transactions were in single lump-sum payments, now or at some time in the

future. However, most situations involve a series of regu-lar payments, for example, car loans and mortgages.

Series compound amount factor: Given a series of regu-lar payments, what will they be worth at some future time?

   Let

 A =the amount of a regular end-of-period payment

Then, note that each payment, A, is compounded for a different period of time. The first payment will be com-pounded for N – 1 periods (yr):