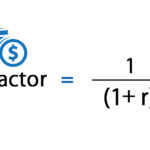Additional concepts involved in interest calculations include continuous cash flow, capitalized costs, begin-ning of period payments, and gradients.

Continuous cash flow: Perhaps the most useful func-tion of continuous interest is its application to situations where the flow of money is of a continuous nature. Con-tinuous cash flow is representative for

1.   A series of regular payments for which the interval be-tween payments is very short

2.   A disbursement at some unknown time (which is then considered to be spread out over the economic period)

Factors for calculating present or future worth of a series of annual amounts, representing the total of a con-tinuous cash flow throughout the year, may be derived by integrating corresponding continuous interest factors over the number of years the flow is maintained.

Continuous cash flow is an appropriate way to han-dle economic evaluations of risk, for example, the present value of an annual expected loss.

Formulas for interest factors representing continu-ous, uniform cash flows are included in Appendix B.

Capitalized costs: Sometimes there are considerations,such as some public works projects, which are considered to last indefinitely and thereby provide perpetual service. For example, how much should a community be willing to invest in a reservoir which will reduce fire insurance costs by some annual amount, A? Taking the limit of the series present worth factor as the number of periods goes to infinity gives the reciprocal of the interest rate. Thus, capitalized costs are just the annual amount divided by theinterest rate. When expressed as an amount required to produce a fixed yield in perpetuity, it is sometimes re-ferred to as an annuity.

Beginning-of-period payments: Most returns on invest-ment (cash inflows) occur at the end of the period during which they accrued. For example, a bank computes and pays interest at the end of the interest period. Accordingly, interest tables, such as those in Appendix C, are computed for end-of-year payments. For example, the values of the capital recovery factor (A/P, i, N) assume that the regular payments, A, occur at the end of each period.

On the other hand, most disbursements (cash out-flows) occur at the beginning of the period (e.g., insurance premiums). When dealing with beginning-of-period pay-ments, it is necessary to make adjustments. One method of adjustment for beginning-of-period payments is to cal-culate a separate set of factors. Another way is to logically interpret the effect of beginning-of-period payments for a particular problem, for example, treating the first pay-ment as a present value. The important thing is to recog-nize that such variations can affect economic analysis.

Gradients: It occasionally becomes necessary to treatthe case of a cash flow which regularly increases or de-creases at each period. Such patterned changes in cash flow are called gradients. They may be a constant amount (linear or arithmetic progression), or they may be a con-stant percentage (exponential or geometric progression). Various equations for dealing with gradient series may be found in Appendix B.