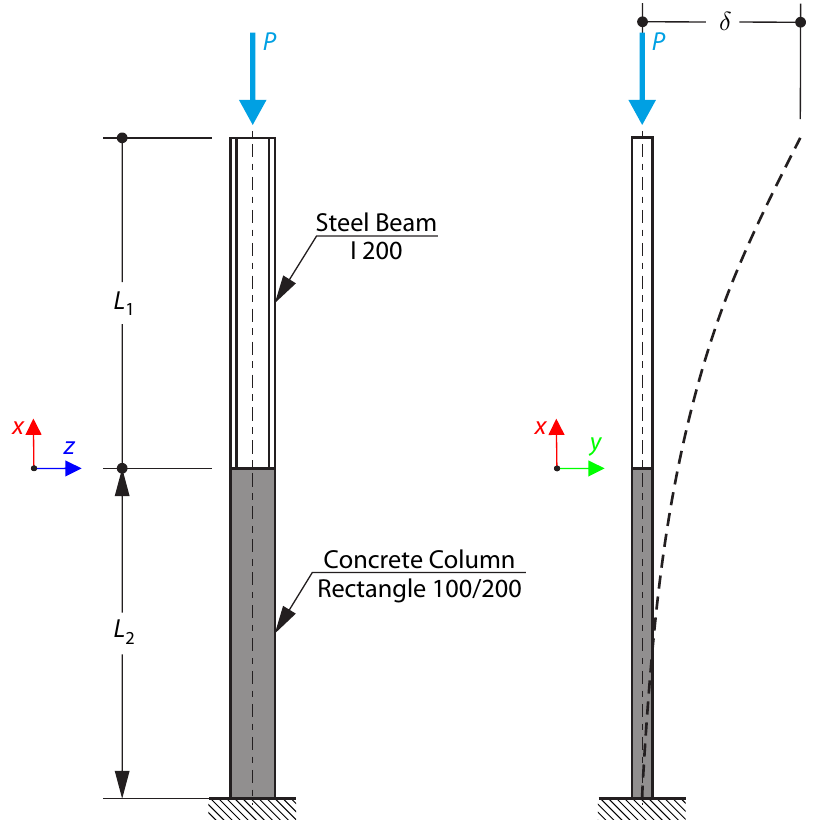
b) Here y-axis is positive towards left and deflection v is positive towards left side
b) From equilibrium of moments about point A, we obtain
From above two equations we will get
Therefore final equation is
General solution
Value of constants is found out from boundary condition which in this case is basically end conditions.
Buckling of pinned-end column in the first mode is called the fundamental case of column buckling. The type of buckling described in this section is called Euler buckling, and the critical load for an ideal elastic column is often called the Euler load.
Boundary condition
From second Boundary condition we will get two cases
Case 1 If 
then 
therefore any value of the quantity kL will satisfy the equation. Consequently, the axial load P may also have any value.
Case 2 The second possibility is given by the following equation, known as the buckling equation
After finding the critical load for a column, we can calculate the corresponding critical stress by dividing the load by the cross-sectional area
Comments are closed.